
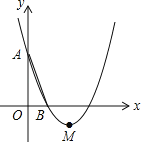
【题目】如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(1)求b、c的值;
(2)若只沿y轴上下平移该抛物线后与y轴的交点为A1,顶点为M1,且四边形AMM1A1是菱形,写出平移后抛物线的表达式.
【答案】(1)b=﹣4,c=3;(2)y=x2﹣4x+3+2![]() 或y=x2﹣4x+3﹣2
或y=x2﹣4x+3﹣2![]() .
.
【解析】
(1)已知抛物线图象上A、B两点的坐标,将它们代入抛物线的解析式中,即可求得m、n的值;
(2)把解析式化成顶点式,求得顶点M的坐标,根据A、M的坐标,易求得AM的长;根据平移的性质知:若四边形A A′B′B为菱形,那么必须满足AA1=AM,由此可确定平移的距离,根据“上加下减”的平移规律即可求得平移后的抛物线解析式.
(1)抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,则有:![]() 解得
解得![]()
故b=﹣4,c=3.
(2)由(1)得:y=x2﹣4x+3=(x﹣2)2﹣1;
∴M(2,﹣1),
∵A(0,3),
∴AM=![]() =2
=2![]() ,
,
由平移可知:AA1∥MM1,AA1=MM1,
当AA1=AM=2![]() 时,四边形AMM1A1是菱形,
时,四边形AMM1A1是菱形,
故抛物线需向上或向下平移2![]() 个单位,即:
个单位,即:
y=x2﹣4x+3+2![]() 或y=x2﹣4x+3﹣2
或y=x2﹣4x+3﹣2![]() .
.


科目:初中数学 来源: 题型:
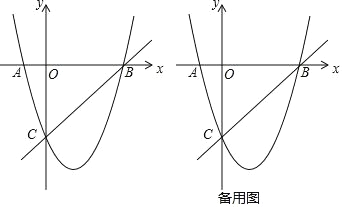
【题目】在平面直角坐标系中,二次函数的图象交坐标轴于 A(﹣1,0),B(4,0),C
(0,﹣4)三点,点 P 是直线 BC 下方抛物线上一动点.
(1) 求这个二次函数的解析式;
(2) 是否存在点 P,使△POC 是以 OC 为底边的等腰三角形?若存在,求出 P 点坐标;若不存在,请说明理由;
(3) 在抛物线上是否存在点 D(与点 A 不重合)使得 S△DBC=S△ABC,若存在,求出点 D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
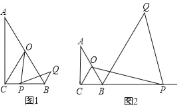
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P顺时针旋转60°,得到线段PQ,连接BQ.
(1)如图1,当点P在线段BC上时,试猜想写出线段CP与BQ的数量关系,并证明你的猜想;
(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?(直接写“成立”或“不成立”即可,不需证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
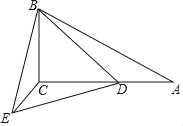
【题目】在Rt△ABC中,∠A=30°,∠ACB=90°,AB=10,D为AC上点.将BD绕点B顺时针旋转60°得到BE,连接CE.
(1)证明:∠ABD=∠CBE;
(2)连接ED,若ED=2![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某粮库需要把晾晒场上的1200t玉米入库封存.
(Ⅰ)入库所需要的时间d(单位:天)与入库平均速度v(单位:t/天)的函数解析式为_____.
(Ⅱ)已知粮库有职工60名,每天最多可入库300t玉米,预计玉米入库最快可在_____天内完成.
(Ⅲ)粮库职工连续工作两天后,天气预报说未来几天会下雨,粮库决定次日把剩下的玉米全部入库,至少需要增加_____名职工.
查看答案和解析>>
科目:初中数学 来源: 题型:
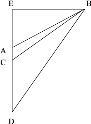
【题目】如图所示,港口A的北偏东60°方向有一个灯塔B,一船上午11时从A出发向正南方向航行,正午12时到达点C处,此时B处恰位于船的北偏东45°方向,则下午什么时间灯塔B位于船的北偏东30°方向?
查看答案和解析>>
科目:初中数学 来源: 题型:
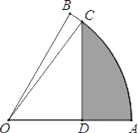
【题目】如图,扇形OAB中,∠AOB=60°,扇形半径为4,点C在![]() 上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为_____.
上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com