
����Ŀ��ij�̳�ͳ����ÿ��ӪҵԱ��ij�µ����۶���������µ�����ͳ��ͼ�Լ�������������ͳ��ͼ��
����������⣺
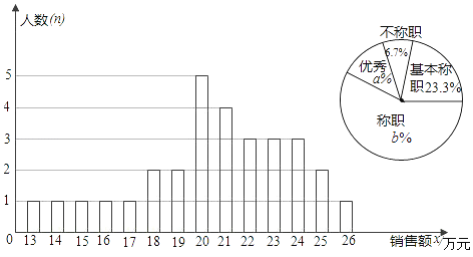
��1����ӪҵԱ�������۶�Ϊx����λ����Ԫ�����̳��涨����x��15ʱΪ����ְ����15��x��20ʱ��Ϊ������ְ����20��x��25Ϊ��ְ����x��25ʱΪ���㣮������ͳ��ͼ�е�a=________��b=________��
��2������ӪҵԱ�����۶����λ���������ֱ��Ƕ��٣�
��3��Ϊ�˵���ӪҵԱ�Ļ����ԣ������ƶ�һ�������۶��������������������ӪҵԱ���ܵ����������Ҫʹ��ӪҵԱ�İ��������ܻ�������Ӧ��Ϊ������Ԫ�������������ɣ�
���𰸡���1��10��60����2����λ��Ϊ21������Ϊ20����3��������Ӧ��Ϊ21��Ԫ�����ɼ�����
�����������������
��1����ͳ��ͼ�е���Ϣ��֪������ְ����2�ˣ�ռ������6.7%���ɴ˿ɵ�������Ϊ��2��6.7%=30���ˣ���������ͳ��ͼ�е���Ϣ��ʾ���������3�ˣ���ְ����18�ˣ��ɴ˿ɵ�3��30��100%=10%��18��30��100%=60%����a=10��b=60��
��2��������ͳ��ͼ��֪���������ݵ�����Ϊ20����λ���ǰ���С���к�ĵ�15��16�����ݵ�ƽ���������ɵ�15��16�����ݶ���21��֪��λ����21��
��3���������֪��������Ӧ�ö�Ϊ21��Ԫ����Ϊ�ɣ�2����֪���������ݵ���λ����21����˰�Ҫʹһ�����ҵ��˻�ý�����Ӧ������λ����Ϊ�����ı�.
���������
��1����ͳ��ͼ����Ϣ�ɵã����̳�����ͳ�Ƶ�ӪҵԱ����=2��6.7%=30���ˣ���
���������3�ˣ�
��a%=3��30��100%=10%��
��a=10��
����ְ����18�ˣ�
��b%=18��30��100%=60%��
��b=60��
��2��������ͳ��ͼ��֪���������ݵ�����Ϊ20��
��������ͳ��ͼ��֪����30�����ݰ���С�������к�15�����͵�16��������21��
���������ݵ���λ��Ϊ21��
��3����Ҫʹһ�����ҵ��˻�ý�����
��������Ӧ������λ��Ϊ��
��������Ӧ��Ϊ21��Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���![]() ��ͼ����y���������ཻ���䶥������Ϊ��
��ͼ����y���������ཻ���䶥������Ϊ��![]() ��1�������н��ۣ���abc��0����a=b����a=4c��4��������
��1�������н��ۣ���abc��0����a=b����a=4c��4��������![]() ��������ȵ�ʵ������������ȷ�Ľ�����______����ֻ����ż��ɣ���
��������ȵ�ʵ������������ȷ�Ľ�����______����ֻ����ż��ɣ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�߶�MN��3cm�����߶�MN��ȡһ��P��ʹPM��PN���ӳ��߶�MN����A��ʹAN��![]() MN���ӳ��߶�NM����B��ʹBN��3BM.
MN���ӳ��߶�NM����B��ʹBN��3BM.
(1)�������⣬����ͼ�Σ�
(2)���߶�AB�ij���
(3)��˵����P����Щ�߶ε��е�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڲ����Ĵ����������ű�������1��2��3��4�Ŀ�Ƭ��С����С�����˰��ո��ԵĹ�����鿨Ƭ��Ϸ��
С��������״ͼ��ͼ��ʾ��
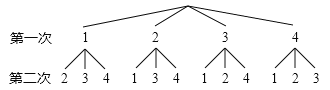
С���г��������£�

�ش��������⣺
��1������С������������ͼ������������Ϸ�����ǣ�������һ�ſ�Ƭ�� �������Ż����������Ż���������������һ�ſ�Ƭ��
��2������С������Ϸ������������ʾ����������Ϊ ��
��3���涨���γ鵽������֮��Ϊ�����Ļ�ʤ������Ϊ˭��ʤ�Ŀ����Դ�Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ϵ�A,B,C��λ����ͼ,��C���߶�AB���е�,��A��ʾ�����ȵ�C��ʾ��������������3,��B�͵�C��ʾ�����ǻ�Ϊ�෴��,��C��ʾ������__________.
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������A1B1C1O��A2B2C2C1��A3B3C3C2����������AnBnnCn��1����ͼ��ʽ���ã���A1��A2��A3������ֱ��y��x+1�ϣ���C1��C2��C3������x���ϣ���֪A1��������ǣ�0��1�������B3������Ϊ_____����Bn��������_____��
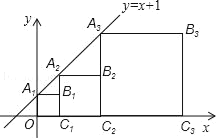
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪O��ֱ��CD�ϵĵ㣬OAƽ�֡�BOC��OEƽ�֡�BOD����AOC=35����

(1) ���BOE�Ķ�����
(2)���COE�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ͬʱ��ѧУ��ѧ�������Ը����Ͷ����ٲ��лؼң��ļ���ѧУ�����������ҵļ���ѧУ�����������Ҽ���ѧУ�ľ���ȼ���ѧУ�ľ���Զ3900�ף�����һ�ؼҾͿ�ʼ��ʲҵ�������ʱ���ִ������ҵ���ϰ�ᣮ����������ȥ�ң�������;�������Ҳ���������ϰ�ᣬȻ��������ǰ���ٶȲ��лؼң������ڼ��е���ͽ�����ҵ��ʱ����Բ��ƣ�����ױ������ص����У���ͼ������֮��ľ���y�������Ǵ�ѧУ������ʱ��x���ӵĺ�����ϵͼ����ļҺ��ҵļ����_____�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy �У���A ������Ϊ��1��0����P �ǵ�һ����������һ�㣬����PO��PA������POA��m�㣬��PAO��n�㣬�����ǰѣ�m�㣬n�㣩������P �ġ�˫�����ꡱ.���磬�㣨1��1���ġ�˫�����ꡱΪ��45�㣬90�㣩.����P��x��ľ���Ϊ![]() ����m+n ����СֵΪ___��
����m+n ����СֵΪ___��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com