
平面直角坐标系 中,原点O是正三角形ABC外接圆的圆心,点A在
中,原点O是正三角形ABC外接圆的圆心,点A在 轴的正半轴上,△ABC的边长为6.以原点O为旋转中心将△ABC沿逆时针方向旋转角,得到△
轴的正半轴上,△ABC的边长为6.以原点O为旋转中心将△ABC沿逆时针方向旋转角,得到△ ,点
,点 、
、 、
、 分别为点A、B、C的对应点.
分别为点A、B、C的对应点.


(1)当=60时,
①请在图1中画出△ ;
;
②若AB分别与 、
、 交于点D、E,则DE的长为_______;
交于点D、E,则DE的长为_______;
(2)如图2,当 ⊥AB时,
⊥AB时, 分别与AB、BC交于点F、G,则点
分别与AB、BC交于点F、G,则点 的坐标为
_____,△FBG的周长为_____,△ABC与△
的坐标为
_____,△FBG的周长为_____,△ABC与△ 重叠部分的面积为_______.
重叠部分的面积为_______.
(1)由旋转角,对应点可画出图像,(2)DE="2"
(3)A′(- ,3) △FBG的周长6,重叠的面积27-9
,3) △FBG的周长6,重叠的面积27-9
【解析】
试题分析:(1)∵在平面直角坐标系XOY中,△ABC是⊙O的外接圆,经中心O旋转60°后,得到△A′B′C′把⊙0平均分成了六份,六个顶点能构成内接正六边形∴各边的交点又构成小的正六边形,∴AB与A′B′的交点为三等份的点,从而得到DE= ×6=2,(2)∵点O是三角形四心重合的点,AB⊥A’B’.可得A’B’ ⊥x轴,在△ABC中可易求OA=2
×6=2,(2)∵点O是三角形四心重合的点,AB⊥A’B’.可得A’B’ ⊥x轴,在△ABC中可易求OA=2 。∴OA’=2
。∴OA’=2 由O,A’与x 轴组成的三角形是特殊的三角形,即30°,60°90°∴A’(-
由O,A’与x 轴组成的三角形是特殊的三角形,即30°,60°90°∴A’(- ,3) ∵BF=A’F, ∴△FBG的周长="AB的边长=6." (3)设BG为x,则FG为
,3) ∵BF=A’F, ∴△FBG的周长="AB的边长=6." (3)设BG为x,则FG为 x,BF为2x. ∴x+
x,BF为2x. ∴x+ x+2x="6" ∴x=(3-
x+2x="6" ∴x=(3- )∴ △ABC的面积-三倍△BFG的面积=重叠的面积=
)∴ △ABC的面积-三倍△BFG的面积=重叠的面积= ×6×3
×6×3 -
- ×3×
×3× (3-
(3- )×(3-
)×(3- )=27-9
)=27-9 .解:(1)①如图所示.
.解:(1)①如图所示.

……………………………………1分
②DE的长为 2 ; ………………………………2分
(2)点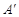 的坐标为
的坐标为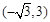 ,△FBG的周长为 6 ,
,△FBG的周长为 6 ,
△ABC与△ 重叠部分的面积为
重叠部分的面积为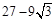 .
.
…………………………………5分
阅卷说明:第(2)问每空1分.
考点:等边三角形的内心定义,旋转图形的性质,三角形外接圆的性质,及直角三角形的性质。
点评:本题有一定的难度,关键熟悉几个公式的应用,由于圆心就是三角形的内心,从而得到特殊角的度数在Rt三角形中,30°所对的直角边是斜边的一半,列出方程求出边长,再有重叠的面积=三角形的面-三个全等的小三角形的面积。注意的是,旋转后得到六个全等的三角形。中档题,有一定的难度,计算量较大易出错。


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:

| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (1)在平面直角坐标系中,描出下列各点:(0,0)、(1,2)、(1,0)、(2,2)、(2,0),并用线段顺次连接各点,你得到了怎样的图案?若各点纵坐标不变,横坐标分别乘以-1,所得的图形与原图形有什么变化?
(1)在平面直角坐标系中,描出下列各点:(0,0)、(1,2)、(1,0)、(2,2)、(2,0),并用线段顺次连接各点,你得到了怎样的图案?若各点纵坐标不变,横坐标分别乘以-1,所得的图形与原图形有什么变化?查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,将凹四边形ABCD称为“基本图形”,且各点的坐标分别为A(4,4),B(l,3),C(3,3),D(3,1).
如图,在平面直角坐标系中,将凹四边形ABCD称为“基本图形”,且各点的坐标分别为A(4,4),B(l,3),C(3,3),D(3,1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com