

 ,求△AGD的面积.
,求△AGD的面积.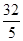
 ∴△ABE≌△BCF(ASA) ··················· ·5分
∴△ABE≌△BCF(ASA) ··················· ·5分 BC,即CF =
BC,即CF = CD = FD,
CD = FD,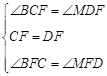 ∴△BCF≌△MDF(ASA)
∴△BCF≌△MDF(ASA)  AM = AD
AM = AD GD·AH=
GD·AH= ×4×
×4× =
=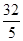 12分
12分

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案科目:初中数学 来源:不详 题型:解答题
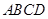 中,点
中,点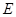 是线段
是线段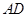 上的任意一点(
上的任意一点(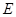 与
与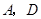 不重合),
不重合),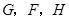 分别是
分别是 的中点.
的中点.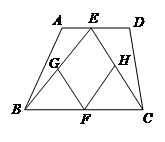
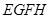 的形状并说明理由;
的形状并说明理由;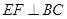 ,且
,且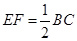 ,证明平行四边形
,证明平行四边形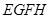 是正方形.
是正方形.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ∥
∥ ,
, ,AB=AD=10cm,BC=8cm.点P从点A出发,以每秒3cm的速度沿折线ABCD方向运动,点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动.已知动点P、Q同时发,当点Q运动到点C时,P、Q运动停止,设运动时间为
,AB=AD=10cm,BC=8cm.点P从点A出发,以每秒3cm的速度沿折线ABCD方向运动,点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动.已知动点P、Q同时发,当点Q运动到点C时,P、Q运动停止,设运动时间为 。
。
 的面积为20
的面积为20 ,若存在,请求出所有满足条件的
,若存在,请求出所有满足条件的 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,AD=
,AD= .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com