
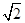 .一动点P从点B出发,沿BC方向以每秒1个单位长度的速度匀速运动,到达点C即停止.在整个运动过程中,过点P作PD⊥BC与Rt△ABC的直角边相交于点D,延长PD至点Q,使得PD=QD,以PQ为斜边在PQ左侧作等腰直角三角形PQE.设运动时间为t秒(t>0).
.一动点P从点B出发,沿BC方向以每秒1个单位长度的速度匀速运动,到达点C即停止.在整个运动过程中,过点P作PD⊥BC与Rt△ABC的直角边相交于点D,延长PD至点Q,使得PD=QD,以PQ为斜边在PQ左侧作等腰直角三角形PQE.设运动时间为t秒(t>0).
 t2,当4<t≤
t2,当4<t≤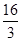 时,S=-
时,S=-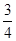 t2+8t-16,当
t2+8t-16,当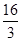 <t<8时,S=
<t<8时,S=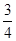 t2-12t+48;(2)
t2-12t+48;(2)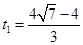 秒或t2=(12-4
秒或t2=(12-4 )秒;(3)8.
)秒;(3)8.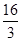 ,当P到C点时t=8,即分为三种情况:根据三角形面积公式求出当0<t≤4时,S=
,当P到C点时t=8,即分为三种情况:根据三角形面积公式求出当0<t≤4时,S= t2,当4<t≤
t2,当4<t≤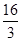 时,S=-
时,S=-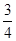 t2+8t-16,当
t2+8t-16,当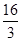 <t<8时,S=
<t<8时,S=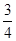 t2-12t+48;
t2-12t+48;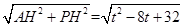 ,
, ,
,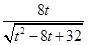 ,若AQ=PQ,得出
,若AQ=PQ,得出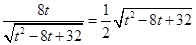 .
.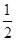 ×2t,求出方程的解即可;
×2t,求出方程的解即可;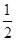 ×CP×AP=8.
×CP×AP=8. t2,当4<t≤
t2,当4<t≤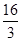 时,S=-
时,S=-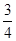 t2+8t-16,当
t2+8t-16,当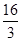 <t<8时,S=
<t<8时,S=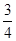 t2-12t+48;(2)存在,理由如下:
t2-12t+48;(2)存在,理由如下: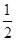 (180°-∠BAC)=45°.
(180°-∠BAC)=45°.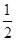 BC=4,AH=BH=4,
BC=4,AH=BH=4,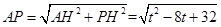 ;
; .
.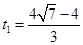 ,
,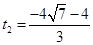 (不合题意,舍去);
(不合题意,舍去);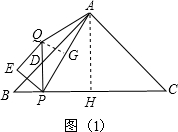
 ,即
,即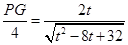 ,
,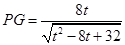 ,
,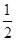 AP,
AP,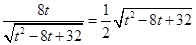 .
. ,t2=12+4
,t2=12+4 (不合题意,舍去);
(不合题意,舍去);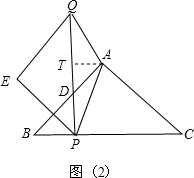
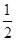 PQ,
PQ,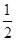 ×2t.解得t=4.
×2t.解得t=4.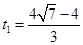 秒或t2=(12-4
秒或t2=(12-4 )秒;
)秒;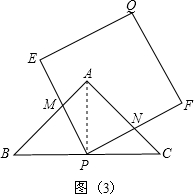
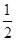 BC,
BC,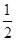 BC=CP=BP=4,∠BAP=∠CAP=
BC=CP=BP=4,∠BAP=∠CAP=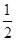 ∠BAC=45°,
∠BAC=45°,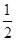 ×CP×AP=
×CP×AP=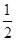 ×4×4=8.
×4×4=8.

科目:初中数学 来源:不详 题型:解答题
 .
.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
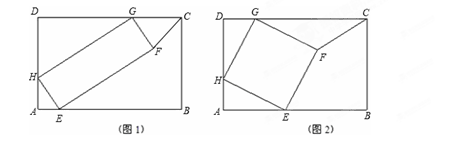
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.120 m | B.100 m | C.75 m | D.25 m |

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
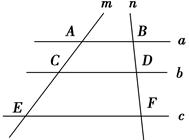
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的值为( )
的值为( )
A. | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com