
【题目】在﹣2,﹣3,4这三个数中任选2个数分别作为点P的横坐标和纵坐标.
(1)可得到的点得个数为 ;
(2)求过P点的正比例函数图象经过第二,四象限的概率(用树形图或列表法求解);
(3)过点P得正比例函数中,函数y随自变量x的增大而增大的概率为 .
【答案】(1)6;(2)![]() ;(3)
;(3)![]()
【解析】解:(1) 6 ;……………………………………………………………………3分
(2)树形图如下:
所经过的6个点分别为
P1(-2,-3)、P2(-2,4)、P3(-3,-2)、
P4(-3,4)、P5(4,-2)、P6(4,-3),……………………………8分
其中经过第二、四象限的共有4个点,………………………………………………9分∴P(经过第二、四象限)=![]() =
=![]() ;……………………………………………10分
;……………………………………………10分
列表法:
(-2,-3) | (-2,4) |
(-3,-2) | (-3,4) |
(4,-2) | (4,-3) |
……………………………………………………………………………………………6分
所经过的6个点分别为
P1(-2,-3)、P2(-2,4)、P3(-3,-2)、
P4(-3,4)、P5(4,-2)、P6(4,-3),……………………………8分
其中经过第二、四象限的共有4个点,………………………………………………9分
∴P(经过第二、四象限)=![]() =
=![]() ;……………………………………………10分
;……………………………………………10分
(3)![]() .……………………………………………………………………………12分
.……………………………………………………………………………12分
根据一次函数的性质,找出符合点正比例函数图象上的点,即可根据概率公式求解


科目:初中数学 来源: 题型:
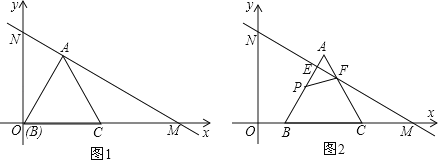
【题目】如图1,在平面直角坐标系xOy中,直线MN分别与x轴正半轴、y轴正半轴交于点M、N,且OM=6cm,∠OMN=30°,等边△ABC的顶点B与原点O重合,BC边落在x轴的正半轴上,点A恰好落在线段MN上,如图2,将等边△ABC从图1的位置沿x轴正方向以1cm/s的速度平移,边AB、AC分别与线段MN交于点E、F,在△ABC平移的同时,点P从△ABC的顶点B出发,以2cm/s的速度沿折线B→A→C运动,当点P达到点C时,点P停止运动,△ABC也随之停止平移.设△ABC平移时间为t(s),△PEF的面积为S(cm2).
(1)求等边△ABC的边长;
(2)当点P在线段BA上运动时,求S与t的函数关系式,并写出自变量t的取值范围;
(3)点P沿折线B→A→C运动的过程中,是否在某一时刻,使△PEF为等腰三角形?若存在,求出此时t值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
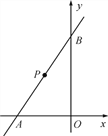
【题目】如图,在平面直角坐标系中,已知直线y=kx+6与x轴、y轴分别交于A,B两点,且△ABO的面积为12.
(1)求k的值;
(2)若点P为直线AB上的一动点,P点运动到什么位置时,△PAO是以OA为底的等腰三角形?求出此时点P的坐标;
(3)在(2)的条件下,连接PO,△PBO是等腰三角形吗?如果是,试说明理由;如果不是,请在线段AB上求一点C,使得△CBO是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,一次函数y=kx+3的图象经过点A(1,4).
(1)求这个一次函数的解析式;
(2)试判断点B(-1,5),C(0,3),D(2,1)是否在这个一次函数的图象上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要从小王和小李两名同学中挑选一人参加全市知识竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表:
次数 | 1 | 2 | 3 | 4 | 5 |
小王 | 60 | 75 | 100 | 90 | 75 |
小李 | 70 | 90 | 100 | 80 | 80 |
根据上表解答下列问题:
(1)完成下表:
姓名 | 平均成绩(分) | 中位数(分) | 众数(分) | 方差 |
小王 | 80 | 75 | 75 | 190 |
小李 |
(2)在这五次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则小王、小李在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为选谁参加比赛比较合适?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国实施的“一带一路”战略方针,惠及沿途各国.中欧班列也已融入其中.从我国重庆开往德国的杜伊斯堡班列,全程约11025千米.同样的货物,若用轮船运输,水路路程是铁路路程的1.6倍,水路所用天数是铁路所用天数的3倍,列车平均日速(平均每日行驶的千米数)是轮船平均日速的2倍少49千米.分别求出列车及轮船的平均日速.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产A、B两种产品共50件,需购买甲、乙两种材料.生产一件A产品需甲种材料30千克、乙种材料10千克;生产一件B产品需甲、乙两种材料各20千克.经测算,购买甲、乙两种材料各1千克共需资金40元,购买甲种材料2千克和乙种材料3千克共需资金105元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过38000元,且生产B产品不少于28件,问符合条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件A产品需加工费200元,生产一件B产品需加工费300元,应选择哪种生产方案,使生产这50件产品的成本最低?(成本=材料费+加工费)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com