【题目】如图，二次函数Y=﹣ 
x2﹣ 
x+2象与x轴交于A、B两点，与y轴交于C点，点D（m，n）是抛物线在第二象限的部分上的一动点，则四边形OCDA的面积的最大值是 ． 
【答案】8
【解析】解：在y=﹣ 
x2﹣ 
x+2中，当x=0时，y=2， ∴C（0，2），
当y=0时，有﹣ x2﹣ x+2=0，解得：x=﹣4或x=1，
∴点A（﹣4，0）、B（1，0），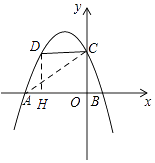
∵点D（m，n）是抛物线在第二象限的部分上的一动点，
∴D（m，﹣ m2﹣ m+2），
过点D作DH⊥x轴于点H，则DH=﹣ m2﹣ m+2，AH=m+4，HO=﹣m，
∵四边形OCDA的面积=△ADH的面积+四边形OCDH的面积，
∴S= （m+4）×（﹣ m2﹣ m+2）+ （﹣ m2﹣ m+2+2）×（﹣m），
=﹣m2﹣4m+4
=﹣（m+2）2+8，（﹣4＜m＜0）；
则m=﹣2时，S取得最大值，最大值为8，
所以答案是：8．
【考点精析】本题主要考查了二次函数的最值和抛物线与坐标轴的交点的相关知识点，需要掌握如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a；一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．才能正确解答此题．
科目：初中数学 来源： 题型：
【题目】请把下列各数填入相应的集合中．
2，0，2π，
，2018，﹣0.030030003…
有理数集合：{___________________________________________…}；
无理数集合：{___________________________________________…}；
非负整数集合：{_________________________________________…}．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠ACB=90°，∠CAD=30°，AC=BC=AD，CE⊥CD，且CE=CD，连接BD、DE、BE,则下列结论：①∠ECA=165°，②BE=BC；③AD=BE；④CD=BD．其中正确的是 （ ）
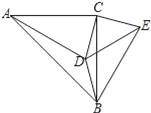
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算：
（1）（5mn2﹣4m2n）（﹣2mn）
（2）（x+7）（x﹣6）﹣（x﹣2）（x+1）
（3） (－
)2 016×161 008；
【答案】（1）﹣10m2n3+8m3n2；（2）2x﹣40；(3)1．
【解析】试题分析：（1）原式利用单项式乘以多项式法则计算即可得到结果；
（2）原式两项利用多项式乘以多项式法则计算，去括号合并即可得到结果；
（3）先根据幂的乘方的逆运算，把(－
)2 016化为(
)1008，再根据积的乘方的逆运算计算即可.
试题解析：（1）原式=（5mn2）（﹣2mn）+（﹣4m2n）（﹣2mn）=﹣10m2n3+8m3n2；
（2）原式=x2﹣6x+7x﹣42﹣x2﹣x+2x+2=2x﹣40．
（3）原式=(
)1008×161 008=(
×16)1 008=1.
【题型】解答题
【结束】
19
【题目】如图，方格图中每个小正方形的边长为1，点A、B、C都是格点．
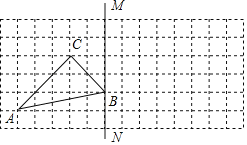
（1）画出△ABC关于直线BM对称的△A1B1C1；
（2）写出AA1的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，一动点从原点O出发，按向上、向右、向下、向右的方向不断地移动，每次移动1个单位长度，得到点A1(0，1)，A2(1，1)，A3(1，0)，A4(2，0)，…，那么点A2 019的坐标为________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，在平面直角坐标系中，点A，B的坐标分别为A(a，0)，B(b，0)，且a，
b满足 |a＋2|＋
＝0，点C的坐标为(0，3).
（1）求a，b的值及S三角形ABC；
（2）若点M在x轴上，且S三角形ACM＝
S三角形ABC，试求点M的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起（其中，∠A=60°，∠D=30°；∠E=∠B=45°）：
（1）①若∠DCE=45°，则∠ACB的度数为 ；
②若∠ACB=140°，求∠DCE的度数；
（2）由（1）猜想∠ACB与∠DCE的数量关系，并说明理由．
（3）当∠ACE＜180°且点E在直线AC的上方时，这两块三角尺是否存在一组边互相平行？若存在，请直接写出∠ACE角度所有可能的值（不必说明理由）；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
