
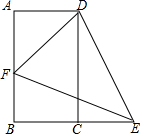
 已知,如图,矩形ABCD,点E是线段BC延长线上一点,且AB=BE,F为边AB上一点,∠DEF=45°.
已知,如图,矩形ABCD,点E是线段BC延长线上一点,且AB=BE,F为边AB上一点,∠DEF=45°.分析 (1)根据矩形的性质结合角的计算即可得出∠CED=60°,在Rt△DCE中利用解直角三角形求出CD、DE的长度,再根据AB=BE以及CE的长度可求出AD的长度,由此即可求出梯形ABED的周长;
(2)延长AB至G,使得BG=CE,由此即可得出△CDE≌△BEG,根据全等三角形的性质找出∠CDE=∠BEG、DE=GE,再通过角的计算即可得出∠GEF=∠DEF,利用全等三角形的判定定理SAS证出△GEF≌△DEF,进而即可得出FD=FG=BF+CE;
(3)解方程17x2+420=169x即可得出BF、CE的长度,设AB=a,即可得出AF、AD的长度,利用勾股定理即可求出a值,再利用勾股定理即可求出DE的长.
解答 解:(1)∵四边形ABCD为矩形,
∴∠B=∠BCD=90°,
∴∠DCE=90°.
∵∠BFE=75°,
∴∠BEF=180°-∠B-∠BFE=15°,
∵∠DEF=45°,
∴∠CED=∠BEF+∠DEF=60°.
在Rt△DCE中,∠DCE=90°,∠CED=60°,CE=3,
∴CD=CE•tan∠CED=3$\sqrt{3}$,DE=$\frac{CE}{cos∠CED}$=6.
∵AB=BE,
∴BE=AB=CD=3$\sqrt{3}$,AD=BC=BE-CE=3$\sqrt{3}$-3,
∴C梯形ABED=AB+BE+ED+DA=3$\sqrt{3}$+3$\sqrt{3}$+6+3$\sqrt{3}$-3=9$\sqrt{3}$+3.
(2)延长AB至G,使得BG=CE,如图1所示.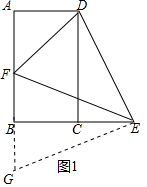
∵AB=BE,AB=CD,
∴CD=BE.
在△CDE和△BEG中,$\left\{\begin{array}{l}{BG=CE}\\{∠EBG=∠DCE=90°}\\{BE=CD}\end{array}\right.$,
∴△CDE≌△BEG(SAS),
∴∠CDE=∠BEG,DE=GE.
∵∠CDE+∠CED=90°,
∴∠GED=∠BEG+∠CED=90°.
∵∠DEF=45°,
∴∠GEF=∠GED-∠DEF=45°=∠DEF.
在△GEF和△DEF中,$\left\{\begin{array}{l}{GE=DE}\\{∠GEF=∠DEF}\\{FE=FE}\end{array}\right.$,
∴△GEF≌△DEF(SAS),
∴FD=FG=FB+BG,
∵BG=CE,
∴FD=BF+CE.
(3)∵线段BF、CE的长是方程17x2+420=169x的两根,且BF<CE,
∴BF=$\frac{84}{17}$,CE=5.
设AB=a(a>0),则AF=AB-BF=a-$\frac{84}{17}$,AD=BE-CE=a-5,
在Rt△DAF中,∠A=90°,AD=a-5,AF=a-$\frac{84}{17}$,DF=BF+CE=$\frac{169}{17}$,
∴DF2=AD2+AF2,即$\frac{28561}{289}$=(a-5)2+$(a-\frac{84}{17})^{2}$,
解得:a=12或a=-$\frac{35}{17}$(舍去),
∴DE=$\sqrt{C{D}^{2}+C{E}^{2}}$=$\sqrt{1{2}^{2}+{5}^{2}}$=13.
点评 本题考查了特殊角的三角函数值、勾股定理以及全等三角形的判定与性质,利用全等三角形的性质找出相等的边角关系是解题的关键.


科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,∠ACB=90,AC=3,BC=4,CD⊥AB,垂足为点D,以点C为圆心,3为半径画圆,则A、B、D三点中在圆外的是B,在圆内的是D,在圆上的是A.
如图,在Rt△ABC中,∠ACB=90,AC=3,BC=4,CD⊥AB,垂足为点D,以点C为圆心,3为半径画圆,则A、B、D三点中在圆外的是B,在圆内的是D,在圆上的是A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,四边形OABC是矩形,OA=16cm,OC=8$\sqrt{2}$cm,两动点M、N分别从O、C同时出发,M在线段OA上沿OA方向以每秒2cm的速度匀速运动,N在线段CO上沿CO方向以每秒$\sqrt{2}$cm的速度匀速运动,设运动时间为t秒(0≤t≤8).
如图,在平面直角坐标系中,四边形OABC是矩形,OA=16cm,OC=8$\sqrt{2}$cm,两动点M、N分别从O、C同时出发,M在线段OA上沿OA方向以每秒2cm的速度匀速运动,N在线段CO上沿CO方向以每秒$\sqrt{2}$cm的速度匀速运动,设运动时间为t秒(0≤t≤8).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,两个正方形ABDE和ACFG如图摆放.
如图,两个正方形ABDE和ACFG如图摆放.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com