Question

某电信公司推出甲、乙两种收费方案供手机用户选择：甲种方案每月收取月租费25元，每分钟通话费为0.2元；乙种方案不收取月租费，每分钟通话费为0.45元．假设每月通话时间为x分钟，甲种方案的每月通话费用为y₁元，乙种方案的每月通话费用为了y₂元．
（1）求每月通话时间x为多少时，甲、乙两种方案的收费相同；
（2）小王计划每月支出通话费用不超过100元，请你根据小王计划每月支出通话费用的多少来帮助他选择合适的方案．

Answer 1

解：（1）由题意知，y₁=25+0.2x，y₂=0.45x
当甲、乙两种方案的收费相同时，25+0.2x=0.45x，
解得x=100；

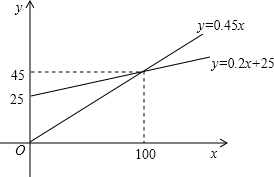
（2）在同一直角坐标系中分别画出这两个函数的图象，由图知：
①当计划每月通话费大于45元时，选择甲方案；
②当计划每月通话费等于45元时，由于甲乙两种方案的收费相同，可在甲、乙两种方案中任选一种；
③当计划每月通话费小于45元时，选择乙方案．
答：（1）每月通话时间x为100分钟，甲、乙两种方案的收费相同；
（2）①当计划每月通话费大于45元时，选择甲方案；
②当计划每月通话费等于45元时，由于甲乙两种方案的收费相同，可在甲、乙两种方案中任选一种；
③当计划每月通话费小于45元时，选择乙方案．
分析：（1）甲种方式是一次函数关系，乙种方式是正比例函数关系．根据题目说明，列出这两个一次函数关系式，求出交点坐标，画出这两个函数图象．
（2）观察图象，分三种情况①当计划每月通话费大于45元时；②当计划每月通话费等于45元时；③当计划每月通话费小于45元时．讨论根据小王计划每月支出通话费，选择最佳方案．
点评：本题是方案选择问题，可以根据通话时间决定的通话费用，进行分情况讨论．