
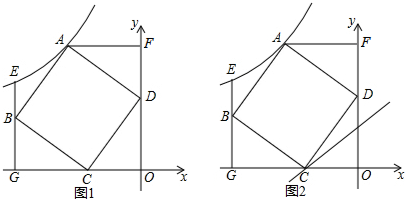
 ����ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��AB=2����ABC=120�㣬����P���߶�BD�ϴӵ�B���D�˶���PE��AB�ڵ�E���ı���PEBF����BD�Գƣ��ı���QGDH���ı���PEBF����AC�Գƣ�������ABCD���������ı��θ�ס���ֵ����ΪS1��BP=x��
����ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��AB=2����ABC=120�㣬����P���߶�BD�ϴӵ�B���D�˶���PE��AB�ڵ�E���ı���PEBF����BD�Գƣ��ı���QGDH���ı���PEBF����AC�Գƣ�������ABCD���������ı��θ�ס���ֵ����ΪS1��BP=x������ ��1������������Ǻ������Էֱ����AO��BO�ij����Ӷ�������öԽ���AC��BD�ij����������ε�������ڶԽ��߳˻���һ�룬�Ӷ�����������ε������
��2��Ҫ�ú�x�Ĵ���ʽ��ʾS1��������������ֱ�д��������������ǵĹ�ϵʽ���ɣ�
��3�����ݣ�2���еĹ�ϵ�����������������x��ֵ��������Խ����
��� �⣺��1��������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��AB=2����ABC=120�㣬
���AOB=90�㣬��ABO=60�㣬
��AO=AB•sin60��=$\sqrt{3}$��BO=AB•cos60��=1��
��AC=2AO=2$\sqrt{3}$��BD=2BO=2��
��${S}_{����ABCD}=\frac{2\sqrt{3}•2}{2}=2\sqrt{3}$��
�ʴ�Ϊ��2$\sqrt{3}$��2$\sqrt{3}$��
��2��������ɵ�
��ABO=60�㣬BP=x����PEB=90�㣬
��BE=BP•cos60��=$\frac{x}{2}$��PE=BP•sin60��=$\frac{\sqrt{3}x}{2}$��
�൱0��x��1ʱ��${S}_{1}=\frac{\frac{1}{2}x•\frac{\sqrt{3}x}{2}}{2}��4$=$\frac{\sqrt{3}{x}^{2}}{2}$��
��1��x��2ʱ��${S}_{1}=\frac{\frac{1}{2}x•\frac{\sqrt{3}x}{2}}{2}��4$-$\frac{2��x-1��•2��\frac{\sqrt{3}}{3}��x-1��}{2}$=$-\frac{\sqrt{3}}{6}{x}^{2}+\frac{4\sqrt{3}x}{3}-\frac{2\sqrt{3}}{3}$��
���Ͽɵã�S1=$\left\{\begin{array}{l}{\frac{\sqrt{3}{x}^{2}}{2}}&{0��x��1}\\{-\frac{\sqrt{3}{x}^{2}}{6}+\frac{4\sqrt{3}x}{3}-\frac{2\sqrt{3}}{3}}&{1��x��2}\end{array}\right.$��
��3������������$2\sqrt{3}$��
����$\frac{\sqrt{3}}{2}{x}^{2}=\sqrt{3}$����x=$\sqrt{2}$��1����ȥ����x=-$\sqrt{2}$����ȥ����
��$-\frac{\sqrt{3}}{6}{x}^{2}+\frac{4\sqrt{3}}{3}x-\frac{2\sqrt{3}}{3}=\sqrt{3}$����x=4$+\sqrt{6}��2$����ȥ������x=4-$\sqrt{6}$��
����P���ƶ�����������S1=$\frac{1}{2}$S����ABCDʱ��x��ֵ��4-$\sqrt{6}$��
���� ���⿼���ı����ۺ��⣬����Ĺؼ�����ȷ���⣬�ҳ�����������Ҫ������������������Ǻ��������ν�ϵ�˼�������⣮


 ��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3��1 | B�� | 2��3 | C�� | 1��2 | D�� | 0��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | AB��CD��AB=CD | B�� | AB��CD��BC��AD | C�� | AB��CD��BC=AD | D�� | AB=CD��BC=AD |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ھ���ABCD�У�AB=4��BC=3����P��CD�����˶�������AP������B��BE��AP������ΪE����AP=x��BE=y�����ܷ�ӳy��x֮�亯����ϵ��ͼ������ǣ�������
��ͼ���ھ���ABCD�У�AB=4��BC=3����P��CD�����˶�������AP������B��BE��AP������ΪE����AP=x��BE=y�����ܷ�ӳy��x֮�亯����ϵ��ͼ������ǣ�������| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��2 | B�� | a��2 | C�� | a��2��a��1 | D�� | a��2��a��1 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com