
分析 由菱形的性质可知AC⊥BD,OD+AO=n①,进而可利用勾股定理得到OD2+OA2=m②,结合①②两式化简即可得到OD•OA的值,再根据菱形的面积公式:两条对角线乘积一半即可得到问题答案.
解答  解:如图所示:
解:如图所示:
∵四边形ABCD是菱形,
∴AO=CO=$\frac{1}{2}$AC,DO=BO=$\frac{1}{2}$BD,AC⊥BD,
∵AC+BD=2n,
∴OD+AO=n①,
∵∠AOB=90°,
∴OD2+OA2=m②,
由①②两式可得n2-2OD•OA=m,
解得:OD•OA=$\frac{{n}^{2}-m}{2}$,
∴BD•AC=2OD•2OA=4OD•OA,
∴菱形面积=$\frac{1}{2}$BD•AC=2n2-2m.
故答案为2n2-2m.
点评 本题考查了菱形的性质、勾股定理的运用以及菱形面积公式的运用,解题的关键是利用整体思想求出OD•OA的值,题目的综合性较强,对学生的计算能力要求较高.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 在如图所示的正方形网格里,以格点为顶点按要求画图,并回答问题.
在如图所示的正方形网格里,以格点为顶点按要求画图,并回答问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
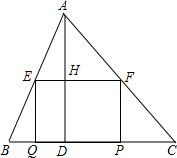 如图,在△ABC中,∠C=45°,BC=10,高AD=8,矩形EFPQ的一边QP在边上,E、F两点分别在AB、AC上,AD交EF于点H.
如图,在△ABC中,∠C=45°,BC=10,高AD=8,矩形EFPQ的一边QP在边上,E、F两点分别在AB、AC上,AD交EF于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
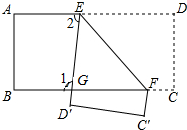 如图,把一张长方形纸片ABCD沿EF折叠后,ED′与BC的交点为G,点D、C分别落在D′、C′的位置上.
如图,把一张长方形纸片ABCD沿EF折叠后,ED′与BC的交点为G,点D、C分别落在D′、C′的位置上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 今年我国多地遭遇雾霾天气,空气污染严重,某地区为绿化环境,计划购买甲、乙两种树苗共计n棵.有关甲、乙两种树苗的信息如图所示.
今年我国多地遭遇雾霾天气,空气污染严重,某地区为绿化环境,计划购买甲、乙两种树苗共计n棵.有关甲、乙两种树苗的信息如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 矩形ABCD中,AB=4,AD=3,P,Q是对角线BD上不重合的两点,点P关于直线AD,AB的对称点分别是E,F,点Q关于直线BC,CD的对称点分别是点G,H,若由点E,F,G,H构成的四边形恰好为菱形,求PQ的长.
矩形ABCD中,AB=4,AD=3,P,Q是对角线BD上不重合的两点,点P关于直线AD,AB的对称点分别是E,F,点Q关于直线BC,CD的对称点分别是点G,H,若由点E,F,G,H构成的四边形恰好为菱形,求PQ的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com