
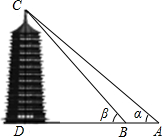
 一数学兴趣小组来到某公园,准备测量一座塔的高度.如图,在A处测得塔顶的仰角为α,在B处测得塔顶的仰角为β,又测量出A、B两点的距离为s米,则塔高为$\frac{tanα•tanβ•s}{tanβ-tanα}$米.
一数学兴趣小组来到某公园,准备测量一座塔的高度.如图,在A处测得塔顶的仰角为α,在B处测得塔顶的仰角为β,又测量出A、B两点的距离为s米,则塔高为$\frac{tanα•tanβ•s}{tanβ-tanα}$米. 分析 在Rt△BCD中有BD=$\frac{CD}{tanβ}$,在Rt△ACD中,根据tan∠A=$\frac{CD}{AD}$=$\frac{CD}{BD+AB}$可得tanα=$\frac{CD}{\frac{CD}{tanβ}+s}$,解之求出CD即可得.
解答 解:在Rt△BCD中,∵tan∠CBD=$\frac{CD}{BD}$,
∴BD=$\frac{CD}{tanβ}$,
在Rt△ACD中,∵tan∠A=$\frac{CD}{AD}$=$\frac{CD}{BD+AB}$,
∴tanα=$\frac{CD}{\frac{CD}{tanβ}+s}$,
解得:CD=$\frac{tanα•tanβ•s}{tanβ-tanα}$,
故答案为:$\frac{tanα•tanβ•s}{tanβ-tanα}$.
点评 本题主要考查解直角三角形的应用-仰角俯角问题,解题的关键是根据两直角三角形的公共边利用三角函数建立方程求解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 当a=1时,函数图象过点(-1,1) | |
| B. | 当a=-2时,函数图象与x轴没有交点 | |
| C. | 若a>0,则当x≥1时,y随x的增大而减小 | |
| D. | 不论a为何值,函数图象必经过(2,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
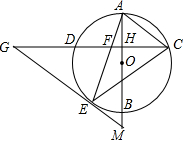 如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过$\widehat{BD}$上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过$\widehat{BD}$上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
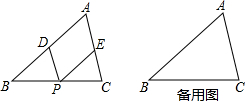 在△ABC中,点P是BC上一动点(与B、C不重合),过点P作PD∥AC交AB于D.作PE∥AB交AC于E,则四边形AEPD是平行四边形.
在△ABC中,点P是BC上一动点(与B、C不重合),过点P作PD∥AC交AB于D.作PE∥AB交AC于E,则四边形AEPD是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
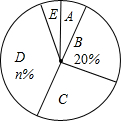 某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.| 类别 | A | B | C | D | E |
| 节目类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
| 人数 | 12 | 30 | m | 54 | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
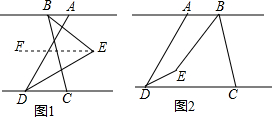
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
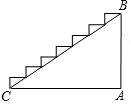 某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为( )
某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为( )| A. | 3.5sin29°米 | B. | 3.5cos29°米 | C. | 3.5tan29°米 | D. | $\frac{3.5}{cos29°}$米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
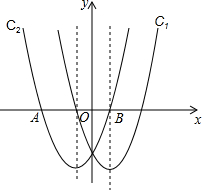 在同一直角坐标系中,抛物线C1:y=ax2-2x-3与抛物线C2:y=x2+mx+n关于y轴对称,C2与x轴交于A、B两点,其中点A在点B的左侧.
在同一直角坐标系中,抛物线C1:y=ax2-2x-3与抛物线C2:y=x2+mx+n关于y轴对称,C2与x轴交于A、B两点,其中点A在点B的左侧.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com