在平面直角坐标系内，已知点Q（10-2a，3-a）在第四象限，a为整数，点P与点Q关于直线y=x对称，
（1）求点Q的坐标；
（2）尺规法作出点P（不写作法保留作图痕迹），并求出点P的坐标（写出计算过程）．
分析：（1）点Q在第四象限，运用坐标系第四象限的性质，可以求出a的取值范围，在根据a是整数，便可确定a值，点Q的坐标便求出来了；
（2）问在第（1）问的基础上，根据对称轴的性质，先确定点P的横坐标，再确定它的纵坐标，便可求出点P的坐标．第二种解法是根据对称轴的性质和两点间的距离公式列出方程，便可求出点P的坐标．
解答：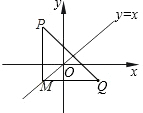
解：（1）∵点Q在第四象限，
∴
，
∴
，（1分）
又∵a是整数，
∴a=4．
∴Q（2，-1）；（1分）
（2）作图（1分）
设直线l：y=x，作QM⊥y轴，交l于点M．
∴M点的纵坐标为-1，
∵点M在l：y=x上，
∴点M（-1，-1）．（2分）
过M作直线PM⊥x轴，截PM=MQ=3，
∴点P（-1，2），（1分）
∵△PMQ是等腰三角形，MO是∠PMQ的平分线，
∴MO垂直且平分PQ．
即P、Q两点关于MO（即直线y=x）对称，此时点P（-1，2）．
点评：综合考查了学生尺规作图的能力，以及有关坐标系．对称轴的知识．
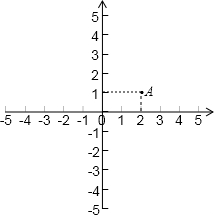在平面直角坐标系内，已知点A（2，1），O为坐标原点．请你在坐标轴上确定点P，使得△AOP成为等腰三角形．在给出的坐标系中把所有这样的点P都找出来，画上实心点，并在旁边标上P1，P2，…，PK的坐标（有k个就标到PK为止，不必写出画法）．