
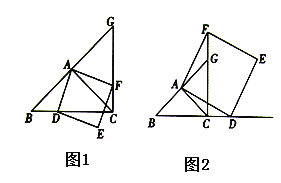
【题目】在![]() 中,
中,![]() ,点
,点![]() 在射线
在射线![]() 上(与
上(与![]() 两点不重合),以
两点不重合),以![]() 为边作正方形
为边作正方形![]() ,使点
,使点![]() 与点
与点![]() 在直线
在直线![]() 的异侧,射线
的异侧,射线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
(1)若点![]() 在线段
在线段![]() 上,如图(1),判断:线段
上,如图(1),判断:线段![]() 与线段
与线段![]() 的数量关系: ,位置关系: .
的数量关系: ,位置关系: .
(2)如图(2),①若点![]() 在线段
在线段![]() 的延长线上,(1)中判断线段
的延长线上,(1)中判断线段![]() 与线段
与线段![]() 的数量关系与位置关系是否仍然成立,并说明理由;
的数量关系与位置关系是否仍然成立,并说明理由;
②当![]() 为
为![]() 中点,
中点,![]() 时,求线段
时,求线段![]() 的长.
的长.
【答案】(1)数量关系:![]() ,位置关系:
,位置关系:![]() ;(2)①仍然成立,证明详见解析;②
;(2)①仍然成立,证明详见解析;② ![]()
【解析】
(1)根据等腰直角三角形的性质得到∠ACB=∠ABC=45°,由正方形的性质得到AD=AF,∠DAF=90°,由角的和差得到∠BAD=∠CAF,推出△BAD≌△CAF(SAS),根据全等三角形的性质得到∠ACF=∠B=45°,BD=CF,证得BC⊥CG,同理△ADC≌△AFG,即可得到结论;
(2)①根据等腰直角三角形的性质得到∠ACB=∠ABC=45°,由正方形的性质得到AD=AF,∠DAF=90°,由角的和差得到∠BAD=∠CAF,推出△BAD≌△CAF(SAS),根据全等三角形的性质得到∠ACF=∠B=45°,BD=CF,证得BC⊥CG,同理△ADC≌△AFG,即可得到结论;②如图(2),过点A作AM⊥BD于M,根据勾股定理可得AD=![]() .
.
(1)数量关系:![]() ,位置关系:
,位置关系:![]() ;
;
∵∠BAC=90°,AB=AC,
∴∠ACB=∠ABC=45°,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°-∠DAC,∠CAF=90°-∠DAC,
∴∠BAD=∠CAF,
则在△BAD和△CAF中,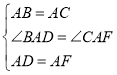 ,
,
∴△BAD≌△CAF(SAS),
∴∠ACF=∠B=45°,BD=CF,
∴∠BCF=∠ACB+∠ACF=90°,
∴BC⊥CG,
同理△ADC≌△AFG,
∴CD=GF,
∴BD+CD=CF+GF,
即BC=CG,
故答案为:BC=CG,BC⊥CG;
(2)①仍然成立
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]() .
.
② 与①同理,可得BD=CF,BC=CG,BC⊥CG,
∵BC=2,G为CF中点,
∴CD=CG=FG=BC=2,
如图(2),过点A作AM⊥BD于M,
∴AM=1,MD=3,
∴AD=![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为民中学租用两辆速度相同的小汽车送1名带队老师和6名学生到城区中学参加数学竞赛,每辆限坐4人(不包括司机).其中一辆小汽车在距离考场16.5 km的地方出现故障,此时离截止进考场的时刻还有50分钟,这时唯一可利用的交通工具是另一辆小汽车,且这辆车的平均速度是55 km/h,人步行的速度是5 km/h(上、下车时间忽略不计).
(1)若小汽车送4人到达考场,然后再回到出故障处接其他人,请你通过计算说明他们能否在截止进考场的时刻前到达考场;
(2)假如你是带队的老师,请设计一种你认为较优的运送方案,使他们能在截止进考场的时刻前到达考场,并通过计算说明方案的可行性.
查看答案和解析>>
科目:初中数学 来源: 题型:
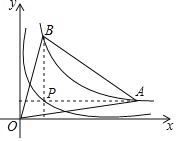
【题目】如图,点P为函数y=![]() (x>0)图象上一点过点P作x轴、y轴的平行线,分别与函数y
(x>0)图象上一点过点P作x轴、y轴的平行线,分别与函数y![]() (x>0)的图象交于点A,B,则△AOB的面积为_____.
(x>0)的图象交于点A,B,则△AOB的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,市民积极参与义务植树活动,小刚同学为了了解自己小区300户家庭在2019年3月义务植树的数量,进行了抽样调查,随机抽取了其中30户家庭,收集的数据如下:(单位:颗)
![]()
(1)对以上数据进行整理、描述和分析
①绘制如下的统计图,请补充完整
②这30户家庭2019年3月份义务植树数量得中位数是 ,众数是 .
(2)“互联网![]() 全民义务植树”是新时代首次全民义务植树组织形式和尽责方式的一大创新,并推出义务植树网上预约服务,小刚同学所调查的这30户家庭有7户家庭采用的网上预约义务植树这种方式,由此可以估计该小区采用这种形式的家庭有多少户?
全民义务植树”是新时代首次全民义务植树组织形式和尽责方式的一大创新,并推出义务植树网上预约服务,小刚同学所调查的这30户家庭有7户家庭采用的网上预约义务植树这种方式,由此可以估计该小区采用这种形式的家庭有多少户?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】首条贯通丝绸之路经济带的高铁线﹣宝兰客专进入全线拉通试验阶段,宝兰客专的通车对加快西北地区与“一带一路”沿线国家和地区的经贸合作、人文交流具有十分重要的意义.试运行期间,一列动车从西安开往西宁,一列普通列车从西宁开往西安,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,根据图象进行一下探究:
【信息读取】
(1)西宁到西安两地相距 千米,两车出发后 小时相遇;
(2)普通列车到达终点共需 小时,普通列车的速度是 千米/小时.
【解决问题】
(3)求动车的速度;
(4)普通列车行驶t小时后,动车到达终点西宁,求此时普通列车还需行驶多少千米到达西安?

查看答案和解析>>
科目:初中数学 来源: 题型:
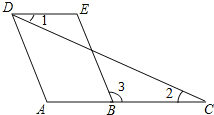
【题目】已知,如图.AD∥BE,∠1=∠2,求证:∠A=∠E.请完成解答过程.
证明:∵AD∥BE(已知)
∴∠A=∠ ( )
又∵∠1=∠2(已知)
∴AC∥ ( )
∴∠3=∠ (两直线平行,内错角相等)
∴∠A=∠E(等量代换)
查看答案和解析>>
科目:初中数学 来源: 题型:
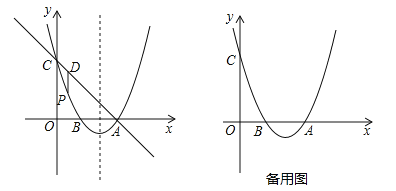
【题目】已知如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与点A重合),过点P作PD∥y轴交直线AC于点D.
(1)求抛物线的解析式;
(2)求点P在运动的过程中线段PD长度的最大值;
(3)△APD能否构成直角三角形?若能请直接写出点P坐标,若不能请说明理由;
(4)在抛物线对称轴上是否存在点M使|MA﹣MC|最大?若存在请求出点M的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
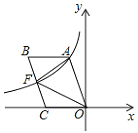
【题目】如图,四边形OABC是平行四边形,边OC在x轴的负半轴上,反比例函数![]() 的图象经过点A与BC的中点F,连接AF,OF,若△AOF的面积为12,则k的值为_______.
的图象经过点A与BC的中点F,连接AF,OF,若△AOF的面积为12,则k的值为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com