
分析 (1)直接确定出里面放入的正方形的个数,即可确定出结论;
(2)分n奇数和偶数两种情况,分别求出可最多放入的正方形的个数,即可确定出结论;
(3)分长方形的长和宽都是偶数,都是奇数,一个偶数,一个奇数,三种情况讨论计算.
解答 解:(1)最多可以放入2个正方形,长方形被覆盖的面积占整个长方形面积的百分比是$\frac{2×{2}^{2}}{4×3}=\frac{2}{3}$≈66.7%;
(2)当n为偶数时,n-2也是偶数,最多可以放入$\frac{1}{4}$n(n-2)个正方形,
长方形被覆盖的面积占整个长方形面积的百分比是100%,
当n为奇数时,n-2也是奇数,最多可放入$\frac{1}{4}$(n-1)(n-3)个正方形,
长方形被覆盖的面积占整个长方形的面积的百分比是$\frac{(n-1)(n-3)}{n(n-2)}×100%$,
(3)设长方形的宽与长分别为x,y,
若x,y都是偶数,则长方形被覆盖的面积占整个长方形面积的100%,不符合题意;
若x,y中一个是偶数2a,一个是奇数(2b+1)(a,b是正整数)
,则$\frac{4ab}{xy}=\frac{4ab}{2a(2b+1)}=\frac{2b}{2b+1}$<0.55,
∴b<0.61,
没有满足此结果的正整数b,这种情况也不符合题意,
因此,x,y都是奇数,
令$\left\{\begin{array}{l}{x=2a+1}\\{y=2b+1}\end{array}\right.$,a≤b,a,b是正整数,
∴$\frac{4ab}{(2a+1)(2b+1)}$<0.55①,
∵$\frac{4ab}{(2a+1)(2b+1)}=\frac{4a}{(2a+1)(2+\frac{1}{b})}$>$\frac{4a}{(2a+1)(2+\frac{1}{a})}=(\frac{2a}{2a+1})^{2}$,
∴$(\frac{2a}{2a+1})^{2}$<0.55,
∴$\frac{2a}{2a+1}<0.74$,
∴a<1.4,
由于a是正整数,
∴a=1.
代入①式,得 $\frac{4b}{3(2b+1)}<0.55$,
解得,b<2.4,
由于b是正整数,
∴b=1或2,
故有x=3,y=3或5,
即:长方形的长为5,宽为3,或长和宽都是3.
点评 此题主要考查了正方形的性质和面积,长方形的性质和面积,分类讨论是解本题的关键也是难点,是一道难度比较大的竞赛题.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
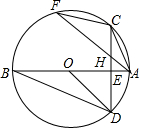 已知,如图,在⊙O中,直径AB=4,点E是OA上任意一点,过点E作弦CD⊥AB,点F是弧AB上的一点,连接AF交CE于点H,连结AC,CF,BD.
已知,如图,在⊙O中,直径AB=4,点E是OA上任意一点,过点E作弦CD⊥AB,点F是弧AB上的一点,连接AF交CE于点H,连结AC,CF,BD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3500(1+x)=4200 | B. | 3500(1-x)+3500(1-x)2=4200 | ||
| C. | 3500(1-x)=4200 | D. | 3500(1-x)2=4200 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -16x-$\frac{1}{2}$ | B. | -16x+$\frac{1}{2}$ | C. | -16x-8 | D. | -16x+8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 可能是锐角三角形 | B. | 不可能是直角三角形 | ||
| C. | 仍然是直角三角形 | D. | 可能是钝角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com