
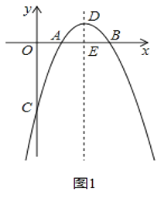
【题目】如图1,抛物线y=ax2+bx﹣3与x轴交于A(1,0)、B两点,与y轴交于点C,抛物线的对称轴为直线x=2,交抛物线于点D,交x轴于点E.
(1)请直接写出:抛物线的函数解析式及点B、点D的坐标;
(2)抛物线对称轴上的一动点P从点D出发,以每秒1个单位的速度向上运动,连接OP,BP,设运动时间为t秒(t>0).在点P的运动过程中,请求出:当t为何值时,∠OPB=90°?
(3)如图2,点Q在抛物线上运动(点Q不与点A、B重合),当△QBC的面积与△ABC的面积相等时,请求出点Q的坐标.
【答案】(1)抛物线的表达式为:y=﹣x2+4x﹣3;B(3,0),D(2,1);(2)t=![]() -1.
-1.
(3)(![]() ,
,![]() )、(
)、(![]() 、
、![]() )或(2,1)
)或(2,1)
【解析】
(1)根据待定系数法即可得到抛物线的表达式,再结合题意即可得到点B、点D的坐标;
(2)假设t秒时,点P(2,1+t),由题意可得OP2=4+(1+t)2,BP2=1+(1+t)2,AB2=9,根据勾股定理可得4+(1+t)2+1+(1+t)2=9,计算即可得到答案.
(3)根据题意算出点Q与BC的距离,求出与BC平行且距离为此距离的平行线的直线方程,与二次函数联立即可求解.
解:(1)抛物线y=ax2+bx﹣3与x轴交于A(1,0),抛物线的对称轴为直线x=2,则点B(3,0),
抛物线的表达式为:y=a(x﹣1)(x﹣3)=a(x2﹣4x+3),
即3a=﹣3,解得:a=﹣1,
故抛物线的表达式为:y=﹣x2+4x﹣3…①,
函数的对称轴为:x=2,则点D(2,1);
(2)t秒时,点P(2,1+t),
则OP2=4+(1+t)2,BP2=1+(1+t)2,AB2=9,
∵∠OPB=90°,则4+(1+t)2+1+(1+t)2=9,
解得:t=![]() -1(负值已舍去).
-1(负值已舍去).
(3)如下图,过点A作BC的平行线交抛物线于点Q、交y轴于点K,
则△QBC的面积与△ABC的面积相等,过点A作AG⊥BC于点G,过点K作KH⊥BC于点H,则AG=KH,
直线BC的倾斜角为45°,则AG=![]() AB=
AB=![]() =KH,
=KH,
则KC=2,故点K(﹣1,0),[来源:.Com]
则直线AQ的函数表达式为:y=x﹣1…②,
联立①②并解得:x=1或2(舍去1),
故点Q(2,1);
在BC的下方与AQ等距离位置作BC的抛物线交抛物线于点Q′、Q″,
同理可得直线Q′Q″的表达式为:y=x﹣5…③,
联立①③并解得:x=![]() ,
,
故点Q(Q′、Q″)的坐标为:(![]() ,
,![]() )、(
)、(![]() 、
、![]() );
);
综上,点Q的坐标为:(![]() ,
,![]() )、(
)、(![]() 、
、![]() )或(2,1).
)或(2,1).


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】宾馆有50间房供游客居住,当每间房每天定价为180元时,宾馆会住满;当每间房每天的定价每增加10元时,就会空闲一间房.如果有游客居住,宾馆需对居住的每间房每天支出20元的费用.当房价定为多少元时,宾馆当天的利润为10890元?设房价比定价180元增加x元,则有( )
A.(x﹣20)(50﹣![]() )=10890B.x(50﹣
)=10890B.x(50﹣![]() )﹣50×20=10890
)﹣50×20=10890
C.(180+x﹣20)(50﹣![]() )=10890D.(x+180)(50﹣
)=10890D.(x+180)(50﹣![]() )﹣50×20=10890
)﹣50×20=10890
查看答案和解析>>
科目:初中数学 来源: 题型:
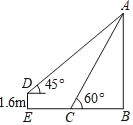
【题目】小明想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好在C处且与地面成60°角,小明拿起绳子末端,后退至E处,拉直绳子,此时绳子末端D距离地面1.6m且绳子与水平方向成45°角.
(1)填空:AD_____AC(填“>”,“<”,“=”).
(2)求旗杆AB的高度.
(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,结果精确到0.1m).
≈1.73,结果精确到0.1m).
查看答案和解析>>
科目:初中数学 来源: 题型:
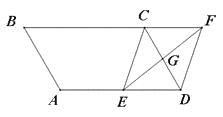
【题目】(7分)如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形;(直接写出答案,不需要说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
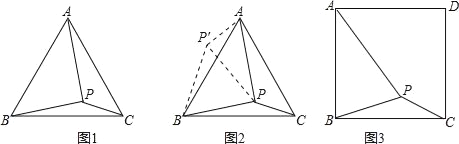
问题:如图1,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.
小刚同学的思路是:将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图2),连接PP′,可得△P′PC是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),所以∠APB=150°,而∠BPC=∠AP′B=150°,进而求出等边△ABC的边长为![]() ,问题得到解决.
,问题得到解决.
请你参考小刚同学的思路,探究并解决下列问题:
如图3,在正方形ABCD内有一点P,且PA=![]() ,BP=2,PC=
,BP=2,PC=![]() .求∠BPC度数的大小和正方形ABCD的边长.
.求∠BPC度数的大小和正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多多班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,下列说法正确的是( )
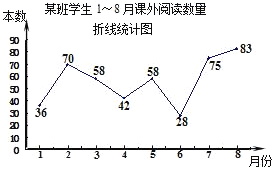
A.极差是47B.众数是42
C.中位数是58D.每月阅读数量超过40的有4个月
查看答案和解析>>
科目:初中数学 来源: 题型:
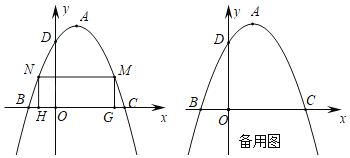
【题目】如图,已知二次函数图象的顶点坐标为![]() ,与坐标轴交于B、C、D三点,且B点的坐标为
,与坐标轴交于B、C、D三点,且B点的坐标为![]() .
.
(1)求二次函数的解析式;
(2)在二次函数图象位于x轴上方部分有两个动点M、N,且点N在点M的左侧,过M、N作x轴的垂线交x轴于点G、H两点,当四边形MNHG为矩形时,求该矩形周长的最大值;
(3)当矩形MNHG的周长最大时,能否在二次函数图象上找到一点P,使![]() 的面积是矩形MNHG面积的
的面积是矩形MNHG面积的![]() ?若存在,求出该点的横坐标;若不存在,请说明理由.
?若存在,求出该点的横坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com