
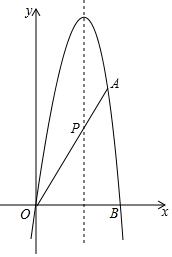
 ������y=-$\sqrt{3}$x2+bx+c������O��0��0����A��4��4$\sqrt{3}$������x�����һ����Ϊ��B���������ߵĶԳ������߶�OA���ڵ�P��
������y=-$\sqrt{3}$x2+bx+c������O��0��0����A��4��4$\sqrt{3}$������x�����һ����Ϊ��B���������ߵĶԳ������߶�OA���ڵ�P������ ��1����O��0��0����A��4��4$\sqrt{3}$�����������y=-$\sqrt{3}$x2+bx+c��ת��Ϊ�ⷽ���鼴�ɣ�
��2�������ֱ��OA�Ľ���ʽ����B���꣬�����ߵĶԳ��ἴ�ɽ�����⣮
��3������ͼ1�У���O����ֱ��BQ�ĶԳƵ�Ϊ��C������Cǡ����ֱ��l��ʱ������֤���ı���BOQC�����Σ���Q��m��$\frac{5\sqrt{3}}{2}$��������OQ=OB=5���ɵ÷���m2+��$\frac{5\sqrt{3}}{2}$��2=52���ⷽ�̼��ɽ�����⣮
����ͼ2�У��������D����BΪԲ��5Ϊ�뾶�ġ�B���˶�����A��D��B����ʱ���߶�AD��С����OD��BQ���ڵ�H�������D��H�������꣬�����ֱ��BH�Ľ���ʽ���ɽ�����⣮
��� �⣺��1����O��0��0����A��4��4$\sqrt{3}$�����������y=-$\sqrt{3}$x2+bx+c��
��$\left\{\begin{array}{l}{c=0}\\{-16\sqrt{3}+4b+c=4\sqrt{3}}\end{array}\right.$�����$\left\{\begin{array}{l}{b=5\sqrt{3}}\\{c=0}\end{array}\right.$��
�������ߵĽ���ʽΪy=-$\sqrt{3}$x2+5$\sqrt{3}$x��
��2��������B��5��0����A��4��4$\sqrt{3}$����
��ֱ��OA�Ľ���ʽΪy=$\sqrt{3}$x��AB=$\sqrt{{1}^{2}+��4\sqrt{3}��^{2}}$=7��
�������ߵĶԳ���x=$\frac{5}{2}$��
��P��$\frac{5}{2}$��$\frac{5\sqrt{3}}{2}$����
��3������ͼ1�У���O����ֱ��BQ�ĶԳƵ�Ϊ��C������Cǡ����ֱ��l��ʱ��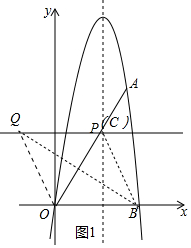
��QC��OB��
���CQB=��QBO=��QBC��
��CQ=BC=OB=5��
���ı���BOQC��ƽ���ı��Σ�
��BO=BC��
���ı���BOQC�����Σ�
��Q��m��$\frac{5\sqrt{3}}{2}$����
��OQ=OB=5��
��m2+��$\frac{5\sqrt{3}}{2}$��2=52��
��m=��$\frac{5}{2}$��
���Q������-$\frac{5}{2}$��$\frac{5\sqrt{3}}{2}$����$\frac{5}{2}$��$\frac{5\sqrt{3}}{2}$��
����ͼ2�У��������D����BΪԲ��5Ϊ�뾶�ġ�B���˶�����A��D��B����ʱ���߶�AD��С����OD��BQ���ڵ�H��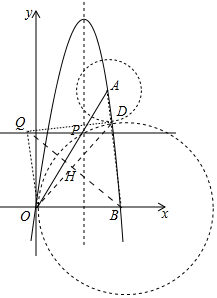
��AB=7��BD=5��
��AD=2��D��$\frac{30}{7}$��$\frac{20\sqrt{3}}{7}$����
��OH=HD��
��H��$\frac{15}{7}$��$\frac{10\sqrt{3}}{7}$����
��ֱ��BH�Ľ���ʽΪy=-$\frac{\sqrt{3}}{2}$x+$\frac{5\sqrt{3}}{2}$��
��y=$\frac{5\sqrt{3}}{2}$ʱ��x=0��
��Q��0��$\frac{5\sqrt{3}}{2}$����
���� ���⿼����κ����ۺ��⡢һ�κ�����Ӧ�á�ƽ���ı��ε��ж������ʡ����ε��ж������ʡ����ɶ�����Բ��֪ʶ������Ĺؼ������������ѧ֪ʶ��ѧ���÷��̵�˼��˼�����⣬ѧ�ṹ��һ�κ��������÷����������꣬�����п�ѹ���⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��-2�� | B�� | ��0��2�� | C�� | ��2��0�� | D�� | ��-2��0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 2 | C�� | 7 | D�� | 2��7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�Ķ�������ֱ�ΪA��4��5����B��2��3����C��5��1����
��ͼ����ABC�Ķ�������ֱ�ΪA��4��5����B��2��3����C��5��1�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
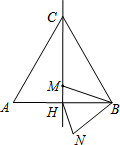 ��ͼ���߳�Ϊ4a�ĵȱ�������ABC�У�M�Ǹ�CH����ֱ���ϵ�һ�����㣬����MB�����߶�BM�Ƶ�B��ʱ����ת60��õ�BN������HN�����ڵ�M�˶������У��߶�HN���ȵ���Сֵ�ǣ�������
��ͼ���߳�Ϊ4a�ĵȱ�������ABC�У�M�Ǹ�CH����ֱ���ϵ�һ�����㣬����MB�����߶�BM�Ƶ�B��ʱ����ת60��õ�BN������HN�����ڵ�M�˶������У��߶�HN���ȵ���Сֵ�ǣ�������| A�� | 2a | B�� | a | C�� | $\frac{1}{2}$a | D�� | $\frac{1}{3}$a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{3}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{1}{4}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com