
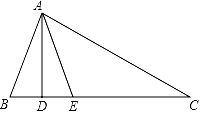
 如图,在△ABC中,AD⊥BC,AE平分∠BAC.
如图,在△ABC中,AD⊥BC,AE平分∠BAC.分析 (1)先根据∠A=80°,∠C=30°,求得∠B的度数,再根据AE平分∠BAC,得到∠BAE的大小.再根据垂直定义,在直角△ABD中,可以求得∠BAD的度数,即可求解∠DAE的大小.
(2)根据AE平分∠BAC,得到∠BAE的大小.再根据垂直定义,在直角△ABD中,可以求得∠BAD的度数,即可求解∠DAE的大小.
(3)根据AE平分∠BAC,得到∠BAE.再根据垂直定义,在直角△ABD中,可以求得∠BAD,即可求得∠DAE=$\frac{1}{2}$(∠B-∠C).
解答  解:(1)∵∠A=80°,∠C=30°,
解:(1)∵∠A=80°,∠C=30°,
∴∠B=70°,
∵AD⊥BC,
∴∠BAD=20°,
∵AE平分∠BAC,
∴∠BAE=$\frac{1}{2}$∠BAC=40°,
∴∠DAE=∠BAE-∠BAD=40°-20°=20°;
(2)∵∠B=80°,
∵AD⊥BC,
∴∠BAD=10°,
∵AE平分∠BAC,
∴∠BAE=$\frac{1}{2}$∠BAC=$\frac{1}{2}$(180°-∠B-∠C)=$\frac{1}{2}$×60°=30°,
∴∠DAE=∠BAE-∠BAD=30°-10°=20°;
(3)能求得∠DAE=$\frac{1}{2}$(∠B-∠C)=20°.
理由:∵AD⊥BC,
∴∠BAD=90°-∠B,
∵AE平分∠BAC,
∴∠BAE=$\frac{1}{2}$∠BAC=$\frac{1}{2}$(180°-∠B-∠C),
∴∠DAE=∠BAE-∠BAD=$\frac{1}{2}$(180°-∠B-∠C)-(90°-∠B)=$\frac{1}{2}$(∠B-∠C)=20°.
点评 主要考查了三角形内角和定理、角平分线的定义和垂直的定义,综合利用了直角三角形的性质.解题时注意:三角形内角和是180°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
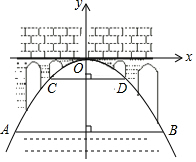 如图,有一座抛物线型拱桥,桥下面在正常水位AB时宽20米,水位上升3米就达到警戒线CD,这时水面宽度为10米.若洪水到来时,水位以每小时0.2米的速度上升从警戒线开始,再持续多少小时才能到拱桥顶?(平面直角坐标系是以桥顶点为点O的)
如图,有一座抛物线型拱桥,桥下面在正常水位AB时宽20米,水位上升3米就达到警戒线CD,这时水面宽度为10米.若洪水到来时,水位以每小时0.2米的速度上升从警戒线开始,再持续多少小时才能到拱桥顶?(平面直角坐标系是以桥顶点为点O的)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +2 | -0.5 | +1.5 | -1.8 | +0.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
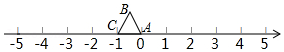 等边△ABC在数轴上的位置如图所示,点A、C对应的数分别为0和-1,若△ABC绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1;则翻转2016次后,点B所对应的数是( )
等边△ABC在数轴上的位置如图所示,点A、C对应的数分别为0和-1,若△ABC绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1;则翻转2016次后,点B所对应的数是( )| A. | 2017 | B. | 2016.5 | C. | 2015.5 | D. | 2015 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 2015 | D. | 2017 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com