
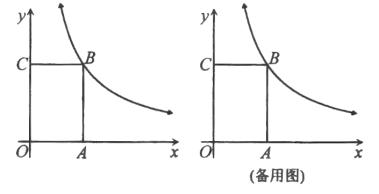
【题目】如图,矩形![]() 的顶点
的顶点![]() 分别在
分别在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在反比例函数
在反比例函数![]() 的第一象限内的图像上,
的第一象限内的图像上,![]() ,动点
,动点![]() 在
在![]() 轴的上方,且满足
轴的上方,且满足![]() .
.
(1)若点![]() 在这个反比例函数的图像上,求点
在这个反比例函数的图像上,求点![]() 的坐标;
的坐标;
(2)连接![]() ,求
,求![]() 的最小值;
的最小值;
(3)若点![]() 是平面内一点,使得以
是平面内一点,使得以![]() 为顶点的四边形是菱形,则请你直接写出满足条件的所有点
为顶点的四边形是菱形,则请你直接写出满足条件的所有点![]() 的坐标.
的坐标.
【答案】(1)点P的坐标为(6,2);(2)![]() ;(3)Q
;(3)Q![]() (4
(4![]() ,5),Q
,5),Q![]() (4+
(4+![]() ,5),Q
,5),Q![]() (42
(42![]() ,1),Q
,1),Q![]() (4+2
(4+2![]() ,1).
,1).
【解析】
(1)首先根据点B坐标,确定反比例函数的解析式,设点P的纵坐标为m(m>0),根据![]() ,构建方程即可解决问题;
,构建方程即可解决问题;
(2)过点(0,2),作直线l⊥y轴,由(1)知,点P的纵坐标为2,推出点P在直线l上作点O关于直线l的对称点O',则OO'=4,连接AO'交直线l于点P,此时PO+PA的值最小;
(3)分两种情形分别求解即可解决问题;
(1)∵四边形OABC是矩形,OA=4,OC=3,
∴点B的坐标为(4,3),
∵点B在反比例函数![]() 的第一象限内的图象上
的第一象限内的图象上
∴k=12,
∴y=![]() ,
,
设点P的纵坐标为m(m>0),
∵![]() .
.
∴![]() OAm=OAOC
OAm=OAOC![]() ,
,
∴m=2,
当点,P在这个反比例函数图象上时,则2=![]() ,
,
∴x=6
∴点P的坐标为(6,2).
(2)过点(0,2),作直线l⊥y轴.

由(1)知,点P的纵坐标为2,
∴点P在直线l上
作点O关于直线l的对称点O',则OO'=4,
连接AO'交直线l于点P,此时PO+PA的值最小,
则PO+PA的最小值=PO'+PA=O'A=![]() .
.
(3)

①如图2中,当四边形ABQP是菱形时,易知AB=AP=PQ=BQ=3,P![]() (4
(4![]() ,2),P
,2),P![]() (4
(4![]() ,2),
,2),
∴Q![]() (4
(4![]() ,5),Q
,5),Q![]() (4+
(4+![]() ,5).
,5).
②如图3中,当四边形ABPQ是菱形时,P![]() (42
(42![]() ,2),P
,2),P![]() (4+2
(4+2![]() ,2),
,2),
∴Q![]() (42
(42![]() ,1),Q
,1),Q![]() (4+2
(4+2![]() ,1).
,1).
综上所述,点Q的坐标为Q![]() (4
(4![]() ,5),Q
,5),Q![]() (4+
(4+![]() ,5),Q
,5),Q![]() (42
(42![]() ,1),Q
,1),Q![]() (4+2
(4+2![]() ,1).
,1).


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】我国明代数学家程大位在他六十岁时终于完成了《外法统宗》的编撰.这是- -木简明实用的数学书,书中列出了许多应用题的数字计算
请从![]() 两题中任选-题做答.
两题中任选-题做答.
![]() :有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差半斤,设所分银子共
:有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差半斤,设所分银子共![]() 两.根据题意列出的方程是____________ .( 注:明代时
两.根据题意列出的方程是____________ .( 注:明代时![]() 两.故有“半斤八两”这个成语)
两.故有“半斤八两”这个成语)
![]() :用九百九十九文钱共买了一千个甜果和苦果.其中四文钱可以买甜果七个,十一文钱可以买苦果九个,设买了
:用九百九十九文钱共买了一千个甜果和苦果.其中四文钱可以买甜果七个,十一文钱可以买苦果九个,设买了![]() 个甜果,根据题意列出的方程是__________.
个甜果,根据题意列出的方程是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年4月8日—11日,博鳌亚洲论坛2018年年会在海南省博鳌镇召开.本届博鳌亚洲论坛的主题为“开放创新的亚洲,繁荣发展的世界”.围绕这一主题,年会设置了“全球化与一带一路”“开放的亚洲”“创新”“改革再出发”四大板块,展开60多场正式讨论.某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区,已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件?
查看答案和解析>>
科目:初中数学 来源: 题型:
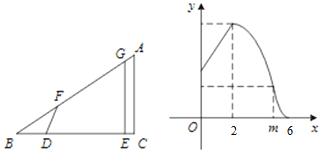
【题目】如图 , ![]() 中,
中, ![]() ,线段
,线段![]() 在射线
在射线![]() 上,且
上,且![]() ,线段
,线段![]() 沿射线
沿射线![]() 运动,开始时,点
运动,开始时,点![]() 与点
与点![]() 重合,点
重合,点![]() 到达点
到达点![]() 时运动停止,过点
时运动停止,过点![]() 作
作![]() ,与射线
,与射线![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 的垂线,与射线
的垂线,与射线![]() 相交于点
相交于点![]() .设
.设![]() ,四边形
,四边形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() 关于
关于![]() 的函数图象如图所示(其中
的函数图象如图所示(其中![]() 时,函数的解析式不同)
时,函数的解析式不同)
(1)填空: ![]() 的长是 ;
的长是 ;
(2)求![]() 关于
关于![]()
![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市某校推进新课改的过程中,开设的体育选修课有:![]() :篮球,
:篮球,![]() :足球,
:足球,![]() :排球,
:排球,![]() :羽毛球,
:羽毛球,![]() :乒乓球,学生可根据自己的爱好选修一门,学校李老师对某班全班同学的选课情况进行调查统计,制成了两幅不完整的统计图(如图).
:乒乓球,学生可根据自己的爱好选修一门,学校李老师对某班全班同学的选课情况进行调查统计,制成了两幅不完整的统计图(如图).

(1)该班学生人数是________,并补全频数分布直方图;
(2)表示“羽毛球”所在扇形的圆心角是________;
(3)若该校共有学生3500名,请估计有多少人选修足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算T,规定:T(x,y)=![]() (其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=
(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=![]() =b.
=b.
(1)已知T(1,﹣1)=﹣2,T(4,2)=1.
①求a,b的值;
②若关于m的不等式组![]() 恰好有3个整数解,求实数p的取值范围;
恰好有3个整数解,求实数p的取值范围;
(2)若T(x,y)=T(y,x)对任意实数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a,b应满足怎样的关系式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,折叠矩形ABCD,使点B落在对角线AC上的点F处,若BC=8,AB=6,则线段CE的长度是( )

A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
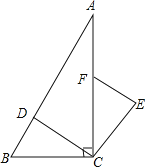
【题目】如图,在Rt△ABC中,∠ACB=90°,点D,F分别在AB,AC上,CF=CB.连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
(1)求证:△BCD≌△FCE;
(2)若EF∥CD.求∠BDC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com