
【题目】如图,在Rt△ABC中,∠C=90°,AB=50,AC=30,D、E、F分别是AC、AB、BC的中点.点P从点D出发沿折线DE﹣EF﹣FC﹣CD以每秒7个单位长的速度匀速运动;点Q从点B出发沿BA方向以每秒4个单位长的速度匀速运动,过点Q作射线QK⊥AB,交折线BC﹣CA于点G.点P、Q同时出发,当点P绕行一周回到点D时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒(t>0).

(1)当点P在DE上,若S△PBQ=![]() ,求t的值.
,求t的值.
(2)当点P运动到折线EF﹣FC上,且点P又恰好落在射线QK上时,求t的值;
(3)连结PG,当PG∥AB时,请直接写出t的值.
【答案】(1)t1=2,t2=![]() ;(2)t1=4
;(2)t1=4![]() ;t2=7
;t2=7![]() ;(3)t1=
;(3)t1=![]() ;t2=7
;t2=7![]() .
.
【解析】
(1)由勾股定理和三角形中位线定理可求DE的长,由锐角三角函数可求PH的长,由三角形面积公式可求解;
(2)①当点P在EF上(![]() ≤t≤5时根据△PQE∽△BCA,根据相似三角形的对应边的比相等,可以求出t的值;
≤t≤5时根据△PQE∽△BCA,根据相似三角形的对应边的比相等,可以求出t的值;
②当点P在FC上(5≤t≤![]() )时,PB=PF+BF就可以得到;
)时,PB=PF+BF就可以得到;
(3)当PG∥AB时四边形PHQG是矩形,由此可以直接写出t.
解:(1)如图1,过点P作PH⊥AB于H,

∵∠C=90°,AB=50,AC=30,
∴BC=![]() =
=![]() =40,
=40,
∵D、E、F分别是AC、AB、BC的中点,
∴DE=![]() BC=20,DE∥BC,EF∥AC,
BC=20,DE∥BC,EF∥AC,
∴∠AED=∠ABC,
∴sin∠AED=sin∠ABC=![]() ,
,
∴![]()
∴PH=![]() (20﹣7t)
(20﹣7t)
∴S△PBQ=![]() ×4t×
×4t×![]() (20﹣7t)=
(20﹣7t)=![]()
∴t1=2,t2=![]() ;
;
(2)①当点P在EF上(![]() ≤t≤5)时,
≤t≤5)时,
如图2,QB=4t,DE+EP=7t,

∵EF∥AC,
∴∠FEB=∠A,且∠PQE=∠ACB,
∴△PQE∽△BCA,
∴![]()
∴![]()
∴t=4![]() ;
;
②当点P在FC上(5≤t≤![]() )时,
)时,
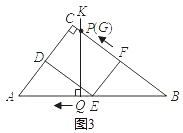
如图3,已知QB=4t,从而PB=![]() =
=![]() =5t,
=5t,
由PF=7t﹣35,BF=20,得5t=7t﹣35+20.
解得t=7![]() ;
;
(3)PG∥AB可分为以下几种情形:
当0<t≤![]() 时,点P下行,点G上行,可知其中存在PG∥AB的时刻,如图4;此后,点G继续上行到点F时,t=4,而点P却在下行到点E再沿EF上行,发现点P在EF上运动时不存在PG∥AB;当5≤t≤
时,点P下行,点G上行,可知其中存在PG∥AB的时刻,如图4;此后,点G继续上行到点F时,t=4,而点P却在下行到点E再沿EF上行,发现点P在EF上运动时不存在PG∥AB;当5≤t≤![]() 时,点P,G均在FC上,也不存在PG∥AB;由于点P比点G先到达点C并继续沿CD下行,所以在
时,点P,G均在FC上,也不存在PG∥AB;由于点P比点G先到达点C并继续沿CD下行,所以在![]() <t<8中存在PG∥AB的时刻,如图5,当8≤t≤10时,点P,G均在CD上,不存在PG∥AB.
<t<8中存在PG∥AB的时刻,如图5,当8≤t≤10时,点P,G均在CD上,不存在PG∥AB.
∴当0<t≤![]() 时,点P下行,点G上行,可知其中存在PG∥AB的时刻,如图4;过点P作PH⊥AB,
时,点P下行,点G上行,可知其中存在PG∥AB的时刻,如图4;过点P作PH⊥AB,
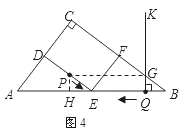
∵PG∥AB,PH∥GQ
∴四边形PGQH是平行四边形,且PH⊥AB,
∴四边形PGQH是矩形,
∴PH=GQ,且∠B=∠AED,∠PHE=∠GQB=90°,
∴△PHE≌△GQB(AAS)
∴HE=QB
∵cos∠AED=cos∠ABC=![]() ,
,
∴![]()
∴HE=![]() (20﹣7t)
(20﹣7t)
∴![]() (20﹣7t)=4t,
(20﹣7t)=4t,
∴t=![]() ;
;
当在![]() <t<8中存在PG∥AB的时刻,如图5,过点P作PH⊥AB,
<t<8中存在PG∥AB的时刻,如图5,过点P作PH⊥AB,

∴四边形PGHQ是矩形,
∴PH=GQ
∵PH=![]() =
=![]() (85﹣7t),GQ=
(85﹣7t),GQ=![]() =
=![]() =3t,
=3t,
∴![]() (85﹣7t)=3t
(85﹣7t)=3t
∴t=7![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,tan∠BAC=2,A(0,a),B(b,0),点C在第二象限,BC与y轴交于点D(0,c),若y轴平分∠BAC,则点C的坐标不能表示为( )
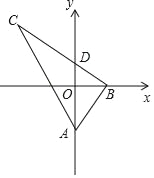
A. (b+2a,2b) B. (﹣b﹣2c,2b)
C. (﹣b﹣c,﹣2a﹣2c) D. (a﹣c,﹣2a﹣2c)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,四边形![]() 是矩形,点
是矩形,点![]() ,点
,点![]() ,点
,点![]() .以
.以![]() 点为中心,顺时针旋转矩形
点为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,点
,点![]() 的对应点分别为
的对应点分别为![]() ,记旋转角为
,记旋转角为![]() .
.
(1)如图①,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;

(2)如图②,当点![]() 落在
落在![]() 的延长线上时,求点
的延长线上时,求点![]() 的坐标;
的坐标;

(3)当点![]() 落在线段
落在线段![]() 上时,求点
上时,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
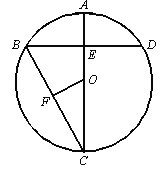
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,
(1)求⊙O的半径;
(2)求O到弦BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是⊙
是⊙![]() 的弦,
的弦,![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 的直线交
的直线交![]() 的延长线于点
的延长线于点![]() ,且
,且![]() 是⊙
是⊙![]() 的切线.
的切线.

(1)判断![]() 的形状,并说明理由;
的形状,并说明理由;
(2)若![]() ,求
,求![]() 的长;
的长;
(3)设![]() 的面积是
的面积是![]() 的面积是
的面积是![]() ,且
,且![]() .若⊙
.若⊙![]() 的半径为
的半径为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学一幢教学楼的顶部竖有一块写有“校训”的宣传牌![]() ,
,![]() 米,王老师用测倾器在
米,王老师用测倾器在![]() 点测得
点测得![]() 点的仰角为
点的仰角为![]() ,再向教学楼前进9米到达
,再向教学楼前进9米到达![]() 点,测得点
点,测得点![]() 的仰角为
的仰角为![]() ,若测倾器的高度
,若测倾器的高度![]()
![]()
![]() 米,不考虑其它因素,求教学楼
米,不考虑其它因素,求教学楼![]() 的高度.(结果保留根号)
的高度.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在BC,CD上,AE=AF,AC与EF相交于点G.下列结论:①AC垂直平分EF;②BE+DF=EF;③当∠DAF=15°时,△AEF为等边三角形;④当∠EAF=60°时,S△ABE=![]() S△CEF.其中正确的是( )
S△CEF.其中正确的是( )
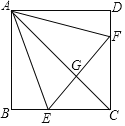
A. ①③B. ②④C. ①③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△EFG中,∠EFG=90°,EF=FG,且点E,F分别在矩形ABCD的边AB,AD上.

(1)如图1,当点G在CD上时,求证:△AEF≌△DFG;
(2)如图2,若F是AD的中点,FG与CD相交于点N,连接EN,求证:EN=AE+DN;
(3)如图3,若AE=AD,EG,FG分别交CD于点M,N,求证:MG2=MNMD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com