
”¾ĢāÄæ”æ“Ó2017Äź1ŌĀ1ČÕĘš£¬ĪŅ¹ś¼ŻŹ»Ö¤æ¼ŹŌÕżŹ½ŹµŹ©ŠĀµÄ¼Żæ¼ÅąŃµÄ£Ź½£¬ŠĀ¹ę¶ØC2¼ŻŹ»Ö¤µÄÅąŃµŃ§Ź±ĪŖ40ѧŹ±£¬¼ŻŠ£µÄѧ·Ń±ź×¼·Ö²»Ķ¬Ź±¶Ī£¬ĘÕĶØŹ±¶ĪaŌŖ/ѧŹ±£¬øß·åŹ±¶ĪŗĶ½Ś¼ŁČÕŹ±¶Ī¶¼ĪŖbŌŖ/ѧŹ±£®
£Ø1£©Š”Ć÷ŗĶŠ”»Ŗ¶¼ŌŚ“Ė¼ŻŠ£²Ī¼ÓC2¼ŻŹ»Ö¤µÄÅąŃµ£¬ĻĀ±ķŹĒŠ”Ć÷ŗĶŠ”»ŖµÄÅąŃµ½įĖć±ķ£ØÅąŃµŃ§Ź±¾łĪŖ40£©£¬ĒėÄćøł¾ŻĢį¹©µÄŠÅĻ¢£¬¼ĘĖć³öa£¬bµÄÖµ£®
ѧŌ± | ÅąŃµŹ±¶Ī | ÅąŃµŃ§Ź± | ÅąŃµ×Ü·ŃÓĆ |
Š”Ć÷ | ĘÕĶØŹ±¶Ī | 20 | 6000ŌŖ |
øß·åŹ±¶Ī | 5 | ||
½Ś¼ŁČÕŹ±¶Ī | 15 | ||
Š”»Ŗ | ĘÕĶØŹ±¶Ī | 30 | 5400ŌŖ |
øß·åŹ±¶Ī | 2 | ||
½Ś¼ŁČÕŹ±¶Ī | 8 |
£Ø2£©Š”³Ā±ØĆū²Ī¼ÓĮĖC2¼ŻŹ»Ö¤µÄÅąŃµ£¬²¢ĒŅ¼Ę»®Ń§¹»Č«²æ»ł±¾Ń§Ź±£¬µ«ĪŖĮĖ²»µ¢Īó¹¤×÷£¬ĘÕĶØŹ±¶ĪµÄÅąŃµŃ§Ź±²»»į³¬¹żĘäĖūĮ½øöŹ±¶Ī×ÜѧŹ±µÄ![]() £¬ČōŠ”³ĀĘÕĶØŹ±¶ĪÅąŃµĮĖxѧŹ±£¬ÅąŃµ×Ü·ŃÓĆĪŖyŌŖ
£¬ČōŠ”³ĀĘÕĶØŹ±¶ĪÅąŃµĮĖxѧŹ±£¬ÅąŃµ×Ü·ŃÓĆĪŖyŌŖ
¢ŁĒóyÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Č·¶Ø×Ō±äĮæxµÄȔֵ·¶Ī§£»
¢ŚŠ”³ĀČēŗĪŃ”ŌńÅąŃµŹ±¶Ī£¬²ÅÄÜŹ¹µĆ±¾“ĪÅąŃµµÄ×Ü·ŃÓĆ×īµĶ£æ
”¾“š°ø”æ£Ø1£©120£¬180£»£Ø2£©¢Ły=-60x+7200£¬0”Üx”Ü![]() £»¢Śx=
£»¢Śx=![]() Ź±£¬yÓŠ×īŠ”Öµ£¬“ĖŹ±y×īŠ”=-60”Į
Ź±£¬yÓŠ×īŠ”Öµ£¬“ĖŹ±y×īŠ”=-60”Į![]() +7200=6400£ØŌŖ£©£®
+7200=6400£ØŌŖ£©£®
”¾½āĪö”æ
£Ø1£©øł¾ŻŠ”Ć÷ŗĶŠ”»ŖµÄÅąŃµ½įĖć±ķĮŠ³ö¹ŲÓŚa”¢bµÄ¶žŌŖŅ»“Ī·½³Ģ×飬½ā·½³Ģ¼“æÉĒó½ā£»
£Ø2£©¢Łøł¾ŻÅąŃµ×Ü·ŃÓĆ=ĘÕĶØŹ±¶ĪÅąŃµ·ŃÓĆ+øß·åŹ±¶ĪŗĶ½Ś¼ŁČÕŹ±¶ĪÅąŃµ·ŃÓĆĮŠ³öyÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£¬½ų¶ųČ·¶Ø×Ō±äĮæxµÄȔֵ·¶Ī§£»
¢Śøł¾ŻŅ»“ĪŗÆŹżµÄŠŌÖŹ½įŗĻ×Ō±äĮæµÄȔֵ·¶Ī§¼“æÉĒó½ā£®
£Ø1£©ÓÉĢāŅā£¬µĆ![]() £¬
£¬
½āµĆ![]() £¬
£¬
¹Źa£¬bµÄÖµ·Ö±šŹĒ120£¬180£»
£Ø2£©¢ŁÓÉĢāŅā£¬µĆy=120x+180£Ø40-x£©£¬
»Æ¼ņµĆy=-60x+7200£¬
”ßĘÕĶØŹ±¶ĪµÄÅąŃµŃ§Ź±²»»į³¬¹żĘäĖūĮ½øöŹ±¶Ī×ÜѧŹ±µÄ![]() £¬
£¬
”ąx”Ü![]() £Ø40-x£©£¬
£Ø40-x£©£¬
½āµĆx”Ü![]() £¬
£¬
ÓÖx”Ż0£¬
”ą0”Üx”Ü![]() £»
£»
¢Ś”ßy=-60x+7200£¬
k=-60£¼0£¬
”ąyĖęxµÄŌö“ó¶ų¼õŠ”£¬
”ąxČ”×ī“óÖµŹ±£¬yÓŠ×īŠ”Öµ£¬
”ß0”Üx”Ü![]() £»
£»
”ąx=![]() Ź±£¬yÓŠ×īŠ”Öµ£¬“ĖŹ±y×īŠ”=-60”Į
Ź±£¬yÓŠ×īŠ”Öµ£¬“ĖŹ±y×īŠ”=-60”Į![]() +7200=6400£ØŌŖ£©£®
+7200=6400£ØŌŖ£©£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖÅäŗĻ”°Ņ»“ųŅ»Ā·”±¹ś¼Ņ³«Ņ飬ijĢśĀ·»õŌĖ¼Æ×°ĻäĪļĮ÷Ō°ĒųÕżŹ½Ęō¶ÆĮĖ2ĘŚĄ©½Ø¹¤³ĢŅ»ĻīµŲ»ł»ł“”¼Ó¹Ģ“¦Ąķ¹¤³ĢÓÉ2”¢8Į½øö¹¤³Ģ¹«Ė¾³Šµ£½ØÉč£¬¼ŗÖŖ2¹¤³Ģ¹«Ė¾µ„¶Ą½ØÉčĶź³É“ĖĻī¹¤³ĢŠčŅŖ180Ģģ![]() ¹¤³Ģ¹«Ė¾µ„¶ĄŹ©¹¤Ģģŗó£¬
¹¤³Ģ¹«Ė¾µ„¶ĄŹ©¹¤Ģģŗó£¬![]() ¹¤³Ģ¹«Ė¾²ĪÓėŗĻ×÷£¬Į½¹¤³Ģ¹«Ė¾ÓÖ¹²Ķ¬Ź©¹¤
¹¤³Ģ¹«Ė¾²ĪÓėŗĻ×÷£¬Į½¹¤³Ģ¹«Ė¾ÓÖ¹²Ķ¬Ź©¹¤![]() ĢģŗóĶź³ÉĮĖ“ĖĻī¹¤³Ģ.
ĢģŗóĶź³ÉĮĖ“ĖĻī¹¤³Ģ.
£Ø1£©Ēó![]() ¹¤³Ģ¹«Ė¾µ„¶Ą½ØÉčĶź³É“ĖĻī¹¤³ĢŠčŅŖ¶ąÉŁĢģ£æ
¹¤³Ģ¹«Ė¾µ„¶Ą½ØÉčĶź³É“ĖĻī¹¤³ĢŠčŅŖ¶ąÉŁĢģ£æ
£Ø2£©ÓÉÓŚŹÜ¹¤³Ģ½ØÉč¹¤ĘŚµÄĻŽÖĘ£¬ĪļĮ÷Ō°Ēų¹ÜĪÆ»į¾ö¶Ø½«“ĖĻī¹¤³Ģ»®°ü³ÉĮ½²æ·Ö£¬ŅŖĒóĮ½¹¤³Ģ¹«Ė¾Ķ¬Ź±æŖ¹¤£¬![]() ¹¤³Ģ¹«Ė¾½ØÉčĘäÖŠŅ»²æ·ÖÓĆĮĖ
¹¤³Ģ¹«Ė¾½ØÉčĘäÖŠŅ»²æ·ÖÓĆĮĖ![]() ĢģĶź³É£¬
ĢģĶź³É£¬![]() ¹¤³Ģ¹«Ė¾½ØÉčĮķŅ»²æ·ÖÓĆĮĖ
¹¤³Ģ¹«Ė¾½ØÉčĮķŅ»²æ·ÖÓĆĮĖ![]() ĢģĶź³É£¬ĘäÖŠ
ĢģĶź³É£¬ĘäÖŠ![]() £¬
£¬![]() ¾łĪŖÕżÕūŹż£¬ĒŅ
¾łĪŖÕżÕūŹż£¬ĒŅ![]() £¬
£¬![]() £¬Ēó
£¬Ēó![]() ”¢
”¢![]() Į½øö¹¤³Ģ¹«Ė¾ø÷Ź©¹¤½ØÉčĮĖ¶ąÉŁĢģ£æ
Į½øö¹¤³Ģ¹«Ė¾ø÷Ź©¹¤½ØÉčĮĖ¶ąÉŁĢģ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¹ŲÓŚxµÄ·½³Ģ£Øx©3£©£Øx©5£©=m£Øm£¾0£©ÓŠĮ½øöŹµŹżøł¦Į£¬¦Ā£Ø¦Į£¼¦Ā£©£¬ŌņĻĀĮŠŃ”ĻīÕżČ·µÄŹĒ£Ø””””£©
A. 3£¼¦Į£¼¦Ā£¼5 B. 3£¼¦Į£¼5£¼¦Ā C. ¦Į£¼2£¼¦Ā£¼5 D. ¦Į£¼3ĒŅ¦Ā£¾5
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
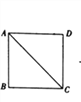
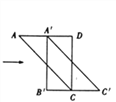
”¾ĢāÄæ”æČēĶ¼£¬½«±ß³¤ĪŖ12µÄÕż·½ŠĪABCDŃŲĘä¶Ō½ĒĻßAC¼ōæŖ£¬ŌŁ°Ń”÷ABCŃŲ×ÅAD·½ĻņĘ½ŅĘ£¬µĆµ½”÷![]() £¬µ±Į½øöČż½ĒŠĪÖŲµžµÄĆ껿ĪŖ32Ź±£¬ŌņĖüŅĘ¶ÆµÄ¾ąĄė
£¬µ±Į½øöČż½ĒŠĪÖŲµžµÄĆ껿ĪŖ32Ź±£¬ŌņĖüŅĘ¶ÆµÄ¾ąĄė![]() µČÓŚ_____.
µČÓŚ_____.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
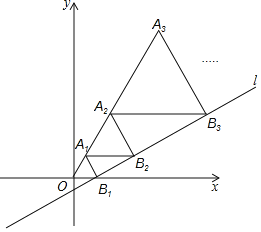
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Ö±Ļßl£ŗy=![]() x-
x-![]() ÓėxÖį½»ÓŚµćB1£¬ŅŌOB1ĪŖ±ß³¤×÷µČ±ßČż½ĒŠĪA1OB1£¬¹żµćA1×÷A1B2Ę½ŠŠÓŚxÖį£¬½»Ö±ĻßlÓŚµćB2£¬ŅŌA1B2ĪŖ±ß³¤×÷µČ±ßČż½ĒŠĪA2A1B2£¬¹żµćA2×÷A2B3Ę½ŠŠÓŚxÖį£¬½»Ö±ĻßlÓŚµćB3£¬ŅŌA2B3ĪŖ±ß³¤×÷µČ±ßČż½ĒŠĪA3A2B3£¬”£¬°““Ė¹ęĀɽųŠŠĻĀČ„£¬ŌņµćA3µÄŗį×ų±źĪŖ______£»µćA2018µÄŗį×ų±źĪŖ______£®
ÓėxÖį½»ÓŚµćB1£¬ŅŌOB1ĪŖ±ß³¤×÷µČ±ßČż½ĒŠĪA1OB1£¬¹żµćA1×÷A1B2Ę½ŠŠÓŚxÖį£¬½»Ö±ĻßlÓŚµćB2£¬ŅŌA1B2ĪŖ±ß³¤×÷µČ±ßČż½ĒŠĪA2A1B2£¬¹żµćA2×÷A2B3Ę½ŠŠÓŚxÖį£¬½»Ö±ĻßlÓŚµćB3£¬ŅŌA2B3ĪŖ±ß³¤×÷µČ±ßČż½ĒŠĪA3A2B3£¬”£¬°““Ė¹ęĀɽųŠŠĻĀČ„£¬ŌņµćA3µÄŗį×ų±źĪŖ______£»µćA2018µÄŗį×ų±źĪŖ______£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬·½øńÖ½ÖŠµÄĆæøöŠ”·½øń¶¼ŹĒ±ß³¤ĪŖ1øöµ„Ī»µÄÕż·½ŠĪ£¬ŌŚ½ØĮ¢Ę½ĆęÖ±½Ē×ų±źĻµŗ󣬔÷ABCµÄ¶„µć¾łŌŚøńµćÉĻ£¬µćCµÄ×ų±źĪŖ£Ø0£¬-1£©£®
£Ø1£©»³ö”÷ABC¹ŲÓŚŌµćO³ÉÖŠŠÄ¶Ō³ĘµÄĶ¼ŠĪ”÷A1B1C1£»
£Ø2£©ŌŚ£Ø1£©µÄĢõ¼žĻĀÖ±½ÓŠ“³öµćA1µÄ×ų±źĪŖ______£»B1µÄ×ų±źĪŖ______£»
£Ø3£©Ēó³ö”÷ABCµÄĆ껿£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
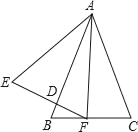
”¾ĢāÄæ”æČēĶ¼£¬½«”÷ABCČʵćCĖ³Ź±ÕėŠż×Ŗ90”ćµĆµ½”÷EDC£®ČōµćA£¬D£¬EŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£¬”ĻACB=20”ć£¬Ōņ”ĻADCµÄ¶ČŹżŹĒ![]() ””””
””””![]()

A. 55”ć B. 60”ć C. 65”ć D. 70”ć
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
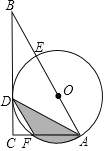
”¾ĢāÄæ”æČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻC=90”ć£¬AB=6£¬ADŹĒ”ĻBACµÄĘ½·ÖĻߣ¬¾¹żA”¢DĮ½µćµÄŌ²µÄŌ²ŠÄOĒ”ŗĆĀäŌŚABÉĻ£¬”ŃO·Ö±šÓėAB”¢ACĻą½»ÓŚµćE”¢F£®Čō”ŃOµÄ°ė¾¶ĪŖ2£®ĒóŅõÓ°²æ·ÖµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCÓė”÷AEFÖŠ£¬AB£½AE£¬BC£½EF£¬”ĻB£½”ĻE£¬AB½»EFÓŚD£®øų³öĻĀĮŠ½įĀŪ£ŗ¢Ł”ĻAFC£½”ĻC£»¢ŚDF£½BF£»¢Ū”÷ADE”×”÷FDB£»¢Ü”ĻBFD£½”ĻCAF£®ĘäÖŠÕżČ·µÄ½įĀŪŹĒ_____£ØĢīŠ“ĖłÓŠÕżČ·½įĀŪµÄŠņŗÅ£©£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com