
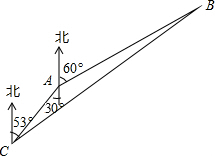
 2016年12月底我国首艘航空母舰辽宁舰与数艘去驱航舰组成编队,携多架歼-15舰载战斗机和多型舰载直升机开展跨海区训练和试验任务,在某次演习中,预警直升机A发现在其北偏东60°,距离160千米处有一可疑目标B,预警直升机立即向位于南偏西30°距离40千米处的航母C报告,航母舰载战斗机立即升空沿北偏东53°方向向可疑目标飞去,请求出舰载战斗机到达目标的航程BC.
2016年12月底我国首艘航空母舰辽宁舰与数艘去驱航舰组成编队,携多架歼-15舰载战斗机和多型舰载直升机开展跨海区训练和试验任务,在某次演习中,预警直升机A发现在其北偏东60°,距离160千米处有一可疑目标B,预警直升机立即向位于南偏西30°距离40千米处的航母C报告,航母舰载战斗机立即升空沿北偏东53°方向向可疑目标飞去,请求出舰载战斗机到达目标的航程BC.分析 如图,过点B向经过点C表示正北方向的直线作垂线,垂足为点D,BD与过点A表示正北方向的直线交于点E,过点A作AF⊥CD于点F,在Rt△ACF中,根据三角函数得出AF,进一步得出DE,再在Rt△ABE中,根据三角函数得出BE,进一步得出BD,再在Rt△BDC中,根据三角函数得出BC即可.
解答 解:如图,过点B向经过点C表示正北方向的直线作垂线,垂足为点D,BD与过点A表示正北方向的直线交于点E,过点A作AF⊥CD于点F, ∵在Rt△ACF中,∠ACF=30°,
∵在Rt△ACF中,∠ACF=30°,
AF=AC•sin∠ACF=10×sin30°=40×$\frac{1}{2}$=20(千米),
∴DE=AF=20(千米),
∵在Rt△ABE中,∠BAE=60°,
BE=AB•sin∠BAE=160×sin60°=160×$\frac{\sqrt{3}}{2}$=80$\sqrt{3}$(千米),
∴BD=DE+BE=20+80$\sqrt{3}$≈158.4(千米),
∴在Rt△BDC中,BC=$\frac{BD}{sin∠BCD}$=$\frac{BC}{sin53°}$≈$\frac{158.4}{0.8}$=198(千米).
故舰载战斗机到达目标的航程BC大约是198千米.
点评 考查了解直角三角形的应用-方向角问题,解答本题的关键是根据方向角构造直角三角形,结合图形利用三角函数的知识解决问题.


科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在△ABC中,AB=AC,∠BAC=150°,点A到BC的距离为1,与AB重合的一条射线AP,从AB开始,以每秒15°的速度绕点A逆时针匀速旋转,到达AC后立即以相同的速度返回AB,到达后立即重复上述旋转过程,设AP与BC边的交点为M,旋转2019秒时,BM=2,CM=2+2$\sqrt{3}$.
在△ABC中,AB=AC,∠BAC=150°,点A到BC的距离为1,与AB重合的一条射线AP,从AB开始,以每秒15°的速度绕点A逆时针匀速旋转,到达AC后立即以相同的速度返回AB,到达后立即重复上述旋转过程,设AP与BC边的交点为M,旋转2019秒时,BM=2,CM=2+2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
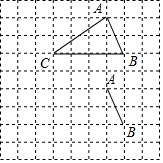 如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券 | 5 | 10 | 5 |
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券 | 10 | 5 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别是ABCD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为2,则平行四边形ABCD的面积为( )
如图,在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别是ABCD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为2,则平行四边形ABCD的面积为( )| A. | 4 | B. | $\frac{3}{10}$ | C. | $\frac{10}{3}$ | D. | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com