
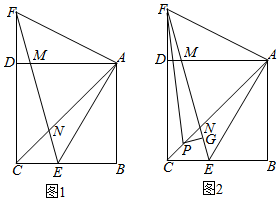
 如图,正方形ABCD中,点E在BC上,点F在CD的延长线上,且EB=DF,连接EF,与AD交于点M,与AC交于点N,连接AE、AF.
如图,正方形ABCD中,点E在BC上,点F在CD的延长线上,且EB=DF,连接EF,与AD交于点M,与AC交于点N,连接AE、AF.分析 (1)根据正方形ABCD的性质,求得CE=2-1=1,CF=1+2=3,再根据勾股定理在Rt△CEF中,求得EF即可;
(2)先判定△AEF是等腰直角三角形,再在FE上截取FO=EN,判定△AON是等边三角形,最后根据FN=FO+NO,得出FN=NE+NA;
(3)先作PH⊥CD于H,PQ⊥CB于Q,连接PE,判定Rt△PFH≌Rt△PFG(HL),Rt△PEQ≌Rt△PEG(HL),进而得出QE=GE,FH=FG,最后根据EF=FG+GE=FH+QE=(CF-CH)+(CE-CQ)进行推导即可得出结论:EF=2AB-2PG.
解答 解:(1)∵正方形ABCD中,AB=CD=2,BE=DF=1,
∴CE=2-1=1,CF=1+2=3,
∴Rt△CEF中,EF=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$;
(2)∵正方形ABCD中,点F在CD的延长线上,
∴∠ADF=∠B=90°,AD=AB,
又∵EB=DF,
∴△ADF≌△ABE(SAS),
∴∠BAE=∠DAF,AE=AF,
又∵∠BAD=∠BAE+∠DAE=90°,
∴∠DAF+∠DAE=90°,即∠EAF=90°,
∴△AEF是等腰直角三角形,
∴∠AFE=∠AEF=45°,
又∵∠ACD=45°,∠CNF=∠ENA,
∴∠CFE=∠EAN,
∴∠BAE=2∠CFE=2∠EAN,
又∵∠BAC=45°,
∴∠EAN=$\frac{1}{3}$∠BAC=15°,
∴∠ANM=∠AEF+∠EAN=45°+15°=60°,
如图1,在FE上截取FO=EN,则△AFO≌△AEN(SAS),
∴AO=AN,
∴△AON是等边三角形,
∴AN=ON,
∵FN=FO+NO,
∴FN=NE+NA;
(3)EF=2AB-2PG.
证明:如图2,作PH⊥CD于H,PQ⊥CB于Q,连接PE,
又∵FP平分∠CFE,PG⊥EF,CP平分∠BCD,
∴PH=PG=PQ=CH=CQ,
又∵PE=PE,PF=PF,
∴Rt△PFH≌Rt△PFG(HL),Rt△PEQ≌Rt△PEG(HL),
∴QE=GE,FH=FG,
∴EF=FG+GE
=FH+QE
=(CF-CH)+(CE-CQ)
=(CD+DF-CH)+(CE-CQ)
=AB+DF-CH+CE-CQ
=AB+DF+CE-2PG
=AB+BE+CE-2PG
=AB+BC-2PG
=2AB-2PG.
点评 本题属于四边形综合题,主要考查了正方形的性质,全等三角形的判定与性质,勾股定理的应用,角平分线的性质,等腰直角三角形以及等边三角形的判定与性质的综合应用,解决问题的关键是作辅助线构造全等三角形以及等边三角形,解题时注意运用线段之间的和差关系进行推导.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
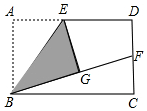 如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点.
如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 年份 | 生活用水量 | 工业用水量 | 农业用水量 | 生态用水量 |
| 2008 | 729.3 | 1397.1 | 3663.5 | 120.2 |
| 2009 | 748.2 | 1390.9 | 3723.1 | 103.0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
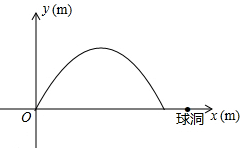 如图,王强在一次高尔夫球的练习中,在某处击球,其飞行路线满足抛物线y=-$\frac{1}{5}$x2+$\frac{16}{5}$x,其中y(m)是球的飞行速度,x(m)是球飞出的水平距离,结果球离球洞的水平距离还有4m.
如图,王强在一次高尔夫球的练习中,在某处击球,其飞行路线满足抛物线y=-$\frac{1}{5}$x2+$\frac{16}{5}$x,其中y(m)是球的飞行速度,x(m)是球飞出的水平距离,结果球离球洞的水平距离还有4m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com