练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．Rt△ABC中，∠C=90°，AC=5，BC=12，则连接两条直角边中点的线段长为（　　）
    A．13B．6.5C．7D．8

    分析 首先利用勾股定理求出斜边AB的长，再根据三角形中位线定理即可求出连结两条直角边中点的线段长．

    解答 解：∵∠C=90°，AC=5，BC=12，
    ∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=13，
    ∴两条直角边中点的线段长=$\frac{1}{2}$AB=6.5，
    故选B．

    点评 此题考查的是勾股定理的运用以及三角形中位线的性质，即三角形的中位线平行于第三边且等于第三边的一半．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    19．下列计算正确的是（　　）
    A．-6+（-3）+（-2）=-1B．7+（-0.5）+2-3=5.5C．-3-3=0D．$（{-1}）-（{-\frac{3}{4}}）+（-4）=3\frac{3}{4}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．单项式-3mx3y的次数为（　　）
    A．3B．4C．3+mD．4+m

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．多项式axy2-$\frac{1}{3}$x与bxy2+$\frac{3}{4}$x的和是一个单项式，则a，b的关系是 （　　）
    A．a=-bB．a=b=0C．a=bD．不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．若$\frac{x}{1×2}$+$\frac{x}{2×3}$+$\frac{x}{3×4}$+…+$\frac{x}{2011×2012}$=2011，则x=2012．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．如图，在△ABC中，D是BC边上的中点，∠BDE=∠CDE，请你添加一个条件，使DE=DF，你添加的条件是∠B=∠C或∠BED=∠CFD（不再添加辅助线和字母）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．在△ABC中，∠C=90°，AC=0.9cm，BC=1.2cm，则斜边上的高CD=0.72．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．下列等式或说法一定正确的是（　　）
    A．$\sqrt{\frac{a}{b}}$=$\frac{\sqrt{a}}{\sqrt{b}}$B．$\sqrt{{a}^{2}-{b}^{2}}$不是最简根式
    C．若a＜0，则$\sqrt{{a}^{4}}$=a2D．$\sqrt{18}$或$\sqrt{48}$是同类二次根式

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

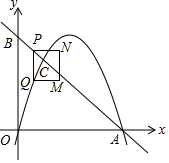    19．如图，在平面直角坐标系中，点A，B分别在x轴，y轴的正半轴上，OA=OB=4，经过点O、A的抛物线y=ax2+bx交AB于点C，点C的横坐标为1，点P在线段AB上，当点P与点A，C均不重合时，过点P与x轴垂直的直线交此抛物线于点Q，以PQ为边向右作矩形PQMN，且PN=1，设点P的横坐标为m．
    （1）求该抛物线所对应的函数解析式；
    （2）当矩形PQMN有两个顶点同时落在此抛物线上时，求点P的坐标；
    （3）设矩形PQMN的周长为d，求d与m之间的函数关系式；并直接写出当d随着m的增大而增大时，m的取值范围．

    查看答案和解析>>

    同步练习册答案