

分析 (1)如图1中,先证明△ABE≌△NCE,再证明FA=FN即可解决问题.
(2)如图2中,延长DG交BA的延长线于点M,连接MC并延长到L使得CL=CD,作FH⊥AD于H,连接KD、KM、KL,先证明△AMG≌△FDG,△KCL≌△KCD,再证明△KDM是等边三角形,最后设AB=a,则DF=AF-2AB=14-2a,∴AD=CF=14-a,DH=7-a,由AF2=AH2+FH2,列出方程即可解决问题.
解答 (1)证明:如图1中,延长AE、FC相交于点N.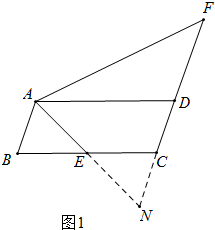
∵四边形ABCD是平行四边形,
∴AB∥DN,
∴∠B=∠ECN,
在△ABE和△HCE中,
$\left\{\begin{array}{l}{∠B=∠ECN}\\{BE=EC}\\{∠AEB=∠CEN}\end{array}\right.$
∴△ABE≌△NCE,
∴CN=AB,∠N=∠BAE=∠FAN,
∴AF=FN=DF+CD+CN=2AB+DF.
(2)解:如图2中,延长DG交BA的延长线于点M,连接MC并延长到L使得CL=CD,作FH⊥AD于H,连接KD、KM、KL,
在△AMG和△FDG中,
$\left\{\begin{array}{l}{∠MAG=∠GFD}\\{AG=GF}\\{∠MGA=∠FGD}\end{array}\right.$
∴△AMG≌△FDG,
∴AM=DF,∵CD=AB,
∴BM=CF=BC,∵∠B=60°,
∴△BCM是等边三角形,
∴∠BCD=∠KCL=120°,
在△KCL和△KCD中,
$\left\{\begin{array}{l}{KC=KC}\\{∠KCL=∠KCD}\\{CL=CD}\end{array}\right.$,
∴△KCL≌△KCD,
∴MG=DG,KL=KD,∠L=∠KDC,∠LKC=∠DKC,
∴KM=KD=KL,
∴∠KMC=∠L=∠KDC,
∴∠DKC+∠KMC=∠LKC+∠L=60°,
∵△BCM是等边三角形,
∴∠BMK+∠KMC=∠BMC=60°,
∴∠BMK=∠DKC,
∴∠MKD=180°-(∠DKC+∠BKM)=180°-(∠BMK+∠BKM)=60°,
∴△KDM是等边三角形,
∴∠BMK+∠KMC=60°=∠KMC+∠CMD,
∴∠BMK=∠CMD,
∴△BMK≌△CMD,
∴BK=CD=AB,设AB=a,则DF=AF-2AB=14-2a,∴AD=CF=14-a,DH=7-a,
由AF2=AH2+FH2,
∴142=(21-2a)2+[$\sqrt{3}$(7-a)]2,整理得到a2-18a+56=0,
解得a=4或14(不合题意舍弃),
∴BE=$\frac{1}{2}$BC=$\frac{1}{2}$(14-a)=5,
∴KE=BE-BK=5-a=1.
点评 本题考查平行四边形的性质、全等三角形的判定和性质等知识,解题的关键是添加辅助线构造全等三角形,学会转化的思想,用方程的思想去思考问题,题目比较难.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:填空题
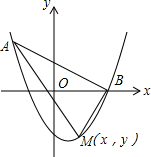 如图,点A(-2,5)在以(1,-4)为顶点的抛物线上,抛物线与x正半轴交于点B,点M(x,y)(其中-2<x<3)是抛物线上的动点,则△ABM面积的最大值为$\frac{125}{8}$.
如图,点A(-2,5)在以(1,-4)为顶点的抛物线上,抛物线与x正半轴交于点B,点M(x,y)(其中-2<x<3)是抛物线上的动点,则△ABM面积的最大值为$\frac{125}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
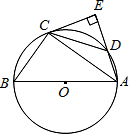 如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.
如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com