
【题目】如图,矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处,折痕AO与边BC交于点O,连结AP、OP.
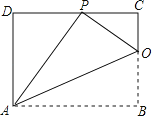
(1)求证:△PDA∽△OCP;
(2)若tan∠PAO=![]() ,求CP的长.
,求CP的长.
【答案】(1)证明见解析;(2)4.
【解析】
(1)由矩形的性质可知∠B=∠C=∠D=90°,由翻折可知,∠APC=90°,利用余角的性质可知∴∠DAP=∠CPO,即可由相似三角形的判定推出结论;
(2)利用正弦函数的定义及相似三角形的性质可直接求出CP的长.
(1)证明:∵四边形ABCD为矩形,
∴∠B=∠C=∠D=90°,
由折叠,可知:∠APO=∠B=90°,
∴∠APD+∠CPO=90°,
∵∠APD+∠DAP=90°,
∴∠DAP=∠CPO,
∴△PDA∽△OCP;
(2)由折叠,可知:∠APO=∠B=90°,AP=AB,PO=BO,
∴tan∠PAO=![]() ,
,
∵△PDA∽△OCP,
∴![]() ,
,
∵AD=8,
∴CP=4.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E是BC的中点,连接DE,过点A作AG⊥ED交DE于点F,交CD于点G.
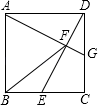
(1)证明:△ADG≌△DCE;(2)连接BF,证明:AB=FB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(问题发现)
如图1,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,延长CA到点F,使得AF=AC,连接DF、BE,则线段BE与DF的数量关系为 ,位置关系为 ;
(2)(拓展研究)
将△ADE绕点A旋转,(1)中的结论有无变化?仅就图(2)的情形给出证明;
(3)(解决问题)
当AB=2,AD=![]() ,△ADE旋转得到D,E,F三点共线时,直接写出线段DF的长.
,△ADE旋转得到D,E,F三点共线时,直接写出线段DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学活动课上,老师带领同学们去测量一座古塔CD的高度.他们首先从A处安置测倾器,测得塔顶C的仰角∠CFE=21°,然后往塔的方向前进50米到达B处,此时测得仰角∠CGE=37°,已知测倾器高1.5米,请你根据以上数据计算出古塔CD的高度.
(参考数据:sin37° ![]() ,tan37°
,tan37° ![]() ,sin21°≈
,sin21°≈![]() ,tan21°≈
,tan21°≈![]() )
)
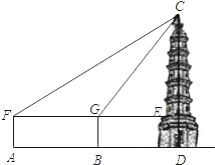
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,以AC为边在△ABC外作等腰△ACD,其中AC=AD.
(1)如图1,若AB为边在△ABC外作△ABE,AB=AE,∠DAC=∠EAB=60°,求∠BFC的度数;
(2)如图2,∠ABC=α,∠ACD=β,BC=4,BD=6.
①若α=30°,β=60°,AB的长为 ;
②若改变α、β的大小,且α+β=90°,求△ABC的面积.
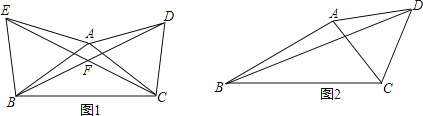
查看答案和解析>>
科目:初中数学 来源: 题型:
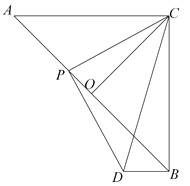
【题目】如图,等腰Rt△ABC的直角边长为![]() ,点O为斜边AB的中点,点P为AB上任意一点,连接PC,以PC为直角边作等腰Rt△PCD,连接BD.
,点O为斜边AB的中点,点P为AB上任意一点,连接PC,以PC为直角边作等腰Rt△PCD,连接BD.
(1)求证: ![]() ;
;
(2)请你判断AC与BD有什么位置关系?并说明理由.
(3)当点P在线段AB上运动时,设AP=x,△PBD的面积为S,求S与x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直于x轴,垂足为点B,反比例函数y=![]() (x>0)的图象经过AO的中点C,交AB于点D,且AD=3.
(x>0)的图象经过AO的中点C,交AB于点D,且AD=3.
(1)设点A的坐标为(4,4)则点C的坐标为 ;
(2)若点D的坐标为(4,n).
①求反比例函数y=![]() 的表达式;
的表达式;
②求经过C,D两点的直线所对应的函数解析式;
(3)在(2)的条件下,设点E是线段CD上的动点(不与点C,D重合),过点E且平行y轴的直线l与反比例函数的图象交于点F,求△OEF面积的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com