
已知正方形ABCD中,M是AB的中点,E是AB延长线上一点,MN⊥DM且交∠CBE的平分线于N,如图.
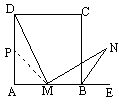
(1)求证:MD=MN;
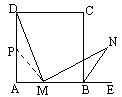
(2)若将上述条件中的“M是AB的中点”改为“M是AB上任意一点”,其余条件不变,如下图,则结论“MD=MN”还成立吗?如果成立,请证明;如果不成立,请说明理由.
|
证明: (1)取AD的中点P,连接PM.∵四边形 ABCD是正方形,∠A=∴∠ ADM+∠DMA=又∵ MN⊥MD,∴∠DMA+∠BMN=又 AP=AM,∴∠APM=∠AMP=且 BN平分∠CBE,∴∠EBN=又 DP=BM=(2)同上可证MD=MN仍成立,证明过程中只是由AP=AM可知DP=BM,可证得△DPM≌△MBN. 分析 (1)在图中,由于M是AB的中点,若取P为AD的中点,可看到△DMP≌△MNB,从而MD=MN.
(2)当M为AB上任意一点时,若在AD上取AP=AM,则可以证得△DMP≌△MNB,同样可以证得MD=MN. |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 如图,已知正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.
如图,已知正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.查看答案和解析>>
科目:初中数学 来源: 题型:
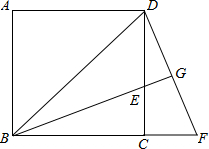 (2012•长沙)如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.
(2012•长沙)如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,已知正方形ABCD中的△DCF可以经过旋转得到△ECB.
如图所示,已知正方形ABCD中的△DCF可以经过旋转得到△ECB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com