
【题目】如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.
(1)求证:DE=DB;
(2)若∠BAC=90°,BD=5,求△ABC外接圆的半径.

【答案】(1)证明见解析(2)![]()
![]()
【解析】试题分析:
(1)由角平分线得出∠ABE=∠CBE,∠BAE=∠CAD,得出![]() ,由圆周角定理得出∠DBC=∠CAD,证出∠DBC=∠BAE,再由三角形的外角性质得出∠DBE=∠DEB,即可得出DE=DB;
,由圆周角定理得出∠DBC=∠CAD,证出∠DBC=∠BAE,再由三角形的外角性质得出∠DBE=∠DEB,即可得出DE=DB;
(2)由(1)得: ![]() ,得出CD=BD=4,由圆周角定理得出BC是直径,∠BDC=90°,由勾股定理求出BC的值,即可得出△ABC外接圆的半径.
,得出CD=BD=4,由圆周角定理得出BC是直径,∠BDC=90°,由勾股定理求出BC的值,即可得出△ABC外接圆的半径.
(1)证明:∵AD平分∠BAC,BE平分∠ABC,
∴∠ABE=∠CBE,∠BAE=∠CAD,
∴![]() ,
,
∴∠DBC=∠CAD,
∴∠DBC=∠BAE,
∵∠DBE=∠CBE+∠DBC,∠DEB=∠ABE+∠BAE,
∴∠DBE=∠DEB,
∴DE=DB;
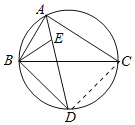
(2)解:连接CD,如图所示:
由(1)得:![]() ,
,
∴CD=BD=5,
∵∠BAC=90°,
∴BC是直径,
∴∠BDC=90°,
∴BC=![]() =5
=5![]() ,
,
∴△ABC外接圆的半径=![]() ×5
×5![]() =
=![]()
![]() .
.


科目:初中数学 来源: 题型:
【题目】下列事件属于必然事件的是( )
A. 掷一枚均匀的硬币,正面朝上B. 车辆行驶到下一路口,遇到绿灯。
C. 若a2=b2,则a=bD. 若|a|>|b|,则a2>b2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题,其中真命题的个数是 ( )
①平行四边形的对边相等; ②;一条对角线平分一组对角的平行四边形是菱形.
③正方形既是轴对称图形,又是中心对称图形; ④对角线相等的四边形是矩形
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为![]() (m2),种草所需费用
(m2),种草所需费用![]() 1(元)与
1(元)与![]() (m2)的函数关系式为
(m2)的函数关系式为 ,其图象如图所示:栽花所需费用
,其图象如图所示:栽花所需费用![]() 2(元)与x(m2)的函数关系式为
2(元)与x(m2)的函数关系式为![]() 2=﹣0.01
2=﹣0.01![]() 2﹣20
2﹣20![]() +30000(0≤
+30000(0≤![]() ≤1000).
≤1000).

(1)请直接写出k1、k2和b的值;
(2)设这块1000m2空地的绿化总费用为W(元),请利用W与![]() 的函数关系式,求出绿化总费用W的最大值;
的函数关系式,求出绿化总费用W的最大值;
(3)若种草部分的面积不少于700m2,栽花部分的面积不少于100m2,请求出绿化总费用W的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com