
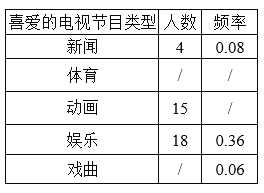
【题目】某校为了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目,以下是根据调查结果绘制的不完整统计表,根据表中信息,回答下列问题:
(1)本次共调查了______名学生;
(2)若将各类电视节目喜爱的人数所占比例绘制成扇形统计图,则“喜爱体育”对应扇形的圆心角度数是_________度;
(3)该校共有1500名学生,根据调查结果估计该校“喜爱体育”节目的学生人数.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
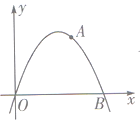
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,
两点,![]() 为抛物线上一点,且横纵坐标相等(原点除外),
为抛物线上一点,且横纵坐标相等(原点除外),![]() 为抛物线上一动点,过
为抛物线上一动点,过![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,并与直线
,并与直线![]() 交于点
交于点![]() .
.
(1)求![]() 、
、![]() 两点的坐标.
两点的坐标.
(2)当点![]() 在线段
在线段![]() 上方时,过
上方时,过![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 相交于点
相交于点![]() ,求
,求![]() 周长的最大值及此时
周长的最大值及此时![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
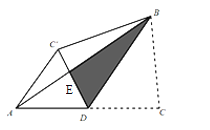
【题目】如图,在△ABC中,D是AC边上的中点,连结BD,把△BDC′沿BD翻折,得到△![]() ,DC与AB交于点E,连结
,DC与AB交于点E,连结![]() ,若AD=AC′=2,BD=3则点D到BC的距离为( )
,若AD=AC′=2,BD=3则点D到BC的距离为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点A、B的坐标分别是A(3,2)、B(1,3).

(1)将△AOB向下平移3个单位后得到△A1O1B1,则点B1的坐标为 ;
(2)将△AOB绕点O逆时针旋转90°后得到△A2OB2,请在图中作出△A2OB2,并求出这时点A2的坐标为 ;
(3)在(2)中的旋转过程中,线段OA扫过的图形的面积 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个整数的个位数字截去,再从余下的数中,减去个位数的2倍,如果差是7的倍数,则原数能被7整除,如果差太大或心算不易看出是否7的倍数,就需要继续上述[截尾、倍大、相减、验差]的过程,直到能清楚判断为止.
例如,判断126是否7的倍数的过程如下:
12﹣6×2=0,0是7的倍数,所以126是7的倍数;
又例如判断6789是否7的倍数的过程如下:
678﹣9×2=660,66﹣0×2=66,66不是7的倍数,所以6789不是7的倍数.
(1)请判断2019和2555是否能被7整除,并说明理由;
(2)有一个千位数字是1的四位正整数,百位数字与十位数字的和是7,个位数字是十位数字的3倍,且这个四位正整数是7的倍数,求这个四位正整数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.
(1)求每张门票原定的票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠措施,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
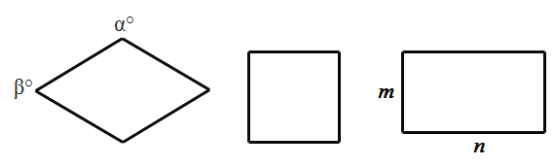
【题目】如图,我们规定菱形与正方形,矩形与正方形的接近程度称为“接近度”,在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设菱形相邻两个内角的度数分别为![]() ,
,![]() ,将菱形的“接近度”定义为
,将菱形的“接近度”定义为![]() ,于是
,于是![]() 越小,菱形越接近正方形.
越小,菱形越接近正方形.
①若菱形的一个内角为![]() ,则该菱形的“接近度”为_________;
,则该菱形的“接近度”为_________;
②当菱形的“接近度”等于_________时,菱形是正方形;
(2)设矩形的长和宽分别为![]() ,
,![]()
![]() ,试写出矩形的“接近度”的合理定义.
,试写出矩形的“接近度”的合理定义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个函数,自变量![]() 取
取![]() 时,函数值
时,函数值![]() 也等于
也等于![]() ,则称
,则称![]() 是这个函数的不动点.
是这个函数的不动点.
已知二次函数![]() .
.
(1)若3是此函数的不动点,则![]() 的值为__________.
的值为__________.
(2)若此函数有两个相异的不动点![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的取值范围为__________.
的取值范围为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是平行四边形ABCD的对角线,DE⊥AB于点E,过点E的直线交BC于点G,且BG=CG.
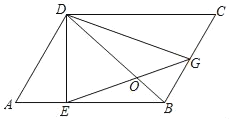
(1)求证:GD=EG.
(2)若BD⊥EG垂足为O,BO=2,DO=4,画出图形并求出四边形ABCD的面积.
(3)在(2)的条件下,以O为旋转中心顺时针旋转△GDO,得到△G′D'O,点G′落在BC上时,请直接写出G′E的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com