
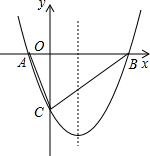
 ��ͼ��������y=ax2-$\frac{3}{2}$x+c��a��0����ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C��0��-2������֪B������Ϊ��4��0����
��ͼ��������y=ax2-$\frac{3}{2}$x+c��a��0����ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C��0��-2������֪B������Ϊ��4��0�������� ��1�����ݵ�B��C���������ô���ϵ����������������ߵĽ���ʽ��
��2���������߽���ʽ��y=0�õ�����x��һԪ���η��̣��ⷽ�����xֵ���ɴ˼��ɵó���A�����꣬���������ľ��빫ʽ�������AC��AB��BC�����ù��ɶ������涨�����ɵó���ABCΪֱ�������Σ��ɴ˼��ɵó���ABC�����Բ��Բ��λ�ã��ٸ��ݵ�A��B�����꼴�����Բ�����ꣻ
��3����ֱ��AB����ƽ�Ƶõ�ֱ��l��ֱ��l��������ֻ��һ������Mʱ����ʱ��M��ֱ��AB�ľ�����Զ�����ݵ�B��C���������ô���ϵ�������ֱ��BC�Ľ���ʽ�����ֱ��l�Ľ���ʽΪy=$\frac{1}{2}$x+m��������������߽���ʽ�����=0���������mֵ��������ֱ��l�������߽���ʽ�ɷ����飬�ⷽ���鼴�������M�����ꣻ
��4��������ڣ����E������Ϊ��n��-n�����Ե�A����B����P����EΪ�����ƽ���ı��η��������������ABΪ�ߣ�����A��B��E��������ʾ��P������꣬��������������߽���ʽ�м������nֵ���Ӷ��ó���E�����ꣻ����ABΪ�Խ��ߣ�����A��B��E��������ʾ��P������꣬��������������߽���ʽ�м������nֵ���Ӷ��ó���E�����꣮���ϼ��ɵó����ۣ�
��� �⣺��1����B��4��0����C��0��-2������y=ax2-$\frac{3}{2}$x+c��a��0���У�
�ã�$\left\{\begin{array}{l}{0=16a-\frac{3}{2}��4+c}\\{-2=c}\end{array}\right.$����ã�$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{c=-2}\end{array}\right.$��
�������ߵĽ���ʽΪy=$\frac{1}{2}$x2-$\frac{3}{2}$x-2��
��2����y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2��x=0����$\frac{1}{2}$x2-$\frac{3}{2}$x-2=0��
��ã�x1=-1��x2=4��
��A��-1��0����
��B��4��0����C��0��-2����
��AC=$\sqrt{5}$��BC=2$\sqrt{5}$��AB=5��
��AC2+BC2=5+20=25=AB2��
���ABCΪֱ�������Σ�
��ABΪ��ABC���Բ��ֱ����
������Բ��Բ��ΪAB���е㣬������Ϊ��$\frac{3}{2}$��0����
��3����ֱ��AB����ƽ�Ƶõ�ֱ��l��ֱ��l��������ֻ��һ������Mʱ����ʱ��M��ֱ��AB�ľ�����Զ����ͼ1��ʾ��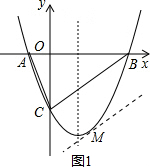
��ֱ��AB�Ľ���ʽΪy=kx+b��ֱ��l�Ľ���ʽΪy=kx+m��
����B��4��0����C��0��-2������y=kx+b��
�ã�$\left\{\begin{array}{l}{0=4k+b}\\{-2=b}\end{array}\right.$����ã�$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-2}\end{array}\right.$��
��ֱ��BC�Ľ���ʽΪy=$\frac{1}{2}$x-2��
��y=$\frac{1}{2}$x+m����y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2����$\frac{1}{2}$x2-$\frac{3}{2}$x-2=$\frac{1}{2}$x+m����$\frac{1}{2}$x2-2x-2-m=0��
��ֱ��l��������ֻ��һ�����㣬
���=��-2��2-4��$\frac{1}{2}$����-2-m��=8+2m=0����ã�m=-4��
��ֱ��l�Ľ���ʽΪy=$\frac{1}{2}$x-4��
����ֱ��l�������߽���ʽ�ã�$\left\{\begin{array}{l}{y=\frac{1}{2}{x}^{2}-\frac{3}{2}x-2}\\{y=\frac{1}{2}x-4}\end{array}\right.$����ã�$\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$��
��M��2��-3����
�ʣ��ǵ�M���߶�BC�ľ���Ϊd����dȡ���ֵʱ�������ʱM�������Ϊ��2��-3����
��4��������ڣ����E������Ϊ��n��-n����
�Ե�A����B����P����EΪ�����ƽ���ı��η������������ͼ2����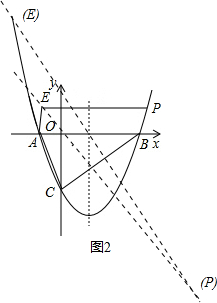
�����߶�ABΪ�ߣ���E�ڵ�P�����ʱ��
��A��-1��0����B��4��0����E��n��-n����
��P��5+n��-n����
�ߵ�P��5+n��-n����������y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2�ϣ�
��-n=$\frac{1}{2}��5+n��^{2}$-$\frac{3}{2}$��5+n��-2����ã�n1=$\frac{-9-\sqrt{57}}{2}$��n2=$\frac{-9+\sqrt{57}}{2}$��
��ʱ��E������Ϊ��$\frac{-9-\sqrt{57}}{2}$��$\frac{9+\sqrt{57}}{2}$����$\frac{-9+\sqrt{57}}{2}$��$\frac{9-\sqrt{57}}{2}$����
���߶�ABΪ�ߣ���E�ڵ�P���ұ�ʱ��
��A��-1��0����B��4��0����E��n��-n����
��P��n-5��-n����
�ߵ�P��n-5��-n����������y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2�ϣ�
��-n=$\frac{1}{2}��n-5��^{2}$-$\frac{3}{2}$��n-5��-2����n2-11n+36=0��
��ʱ��=��-11��2-4��36=-23��0�������⣻
�����߶�ABΪ�Խ���ʱ��
��A��-1��0����B��4��0����E��n��-n����
��P��3-n��n����
�ߵ�P��3-n��n����������y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2�ϣ�
��n=$\frac{1}{2}��3-n��^{2}$-$\frac{3}{2}$��3-n��-2����ã�n3=$\frac{5+\sqrt{41}}{2}$��n4=$\frac{5-\sqrt{41}}{2}$��
��ʱ��E������Ϊ��$\frac{5+\sqrt{41}}{2}$��$\frac{-5-\sqrt{41}}{2}$����$\frac{5-\sqrt{41}}{2}$��$\frac{-5+\sqrt{41}}{2}$����
���Ͽ�֪�����ڵ�P��E��ʹ�Ե�A����B����P����EΪ������ı�����ƽ���ı��Σ���E����Ϊ��$\frac{-9-\sqrt{57}}{2}$��$\frac{9+\sqrt{57}}{2}$������$\frac{-9+\sqrt{57}}{2}$��$\frac{9-\sqrt{57}}{2}$������$\frac{5+\sqrt{41}}{2}$��$\frac{-5-\sqrt{41}}{2}$����$\frac{5-\sqrt{41}}{2}$��$\frac{-5+\sqrt{41}}{2}$����
���� ���⿼���˴���ϵ������������ʽ��ֱ�������ε��ж��������б�ʽ�Լ��ȱ������ε����ʣ�����Ĺؼ��ǣ���1�����ô���ϵ���������������ʽ����2��֤����ABCΪֱ�������Σ���3���ҳ���M��λ�ã���4����ABΪ�ߺ�ABΪ�Խ�������������ǣ����������е��⣬��4���е��Ѷȣ������С��ʱ����ABΪ�ߺ�ABΪ�Խ�������������ǣ��ٸ��ݵȱ������ε����ʽ���������������ҳ���һ���������ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ����ƽ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O����E��BC���е㣮��OE=3����AB=6��
��ͼ��ʾ����ƽ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O����E��BC���е㣮��OE=3����AB=6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m��1 | B�� | m��-1 | C�� | m��1 �� m��-1 | D�� | m��1�� m��-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{\begin{array}{l}{x+y=12}\\{12%x+8%y=14}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{x+y=12}\\{��1+12%��x+��1+8%��y=14}\end{array}\right.$ | ||
| C�� | $\left\{\begin{array}{l}{x+y=14}\\{12%x+8%y=12}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{x+y=14}\\{��1+12%��x+��1+8%��y=12}\end{array}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com