
【题目】有一块矩形地块![]() ,
,![]() 米,
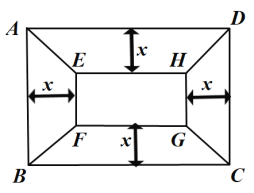
米,![]() 米,为美观,拟种植不同的花卉,如图所示,将矩形
米,为美观,拟种植不同的花卉,如图所示,将矩形![]() 分割成四个等腰梯形及一个矩形,其中梯形的高相等,均为
分割成四个等腰梯形及一个矩形,其中梯形的高相等,均为![]() 米.现决定在等腰梯形
米.现决定在等腰梯形![]() 和
和![]() 中种植甲种花卉;在等腰梯形
中种植甲种花卉;在等腰梯形![]() 和
和![]() 中种植乙种花卉;在矩形
中种植乙种花卉;在矩形![]() 中种植丙种花卉.甲、乙、丙三种花卉的种植成本分别为20元/米
中种植丙种花卉.甲、乙、丙三种花卉的种植成本分别为20元/米![]() 、60 元/米
、60 元/米![]() 、40元/米
、40元/米![]() ,设三种花卉的种植总成本为
,设三种花卉的种植总成本为![]() 元.
元.
(1)当![]() 时,求种植总成本
时,求种植总成本![]() ;
;
(2)求种植总成本![]() 与
与![]() 的函数表达式,并写出自变量
的函数表达式,并写出自变量![]() 的取值范围;
的取值范围;
(3)若甲、乙两种花卉的种植面积之差不超过120米![]() ,求三种花卉的最低种植总成本.
,求三种花卉的最低种植总成本.
科目:初中数学 来源: 题型:
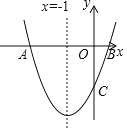
【题目】如图,已知抛物线y=x2+bx+c与x轴交于A、B两点,交y轴于点C,AB=4,对称轴是直线x=﹣1.
(1)求抛物线的解析式及点C的坐标;
(2)连接AC,E是线段OC上一点,点E关于直线x=﹣1的对称点F正好落在AC上,求点F的坐标;
(3)动点M从点O出发,以每秒2个单位长度的速度向点A运动,到达点A即停止运动,过点M作x轴的垂线交抛物线于点N,交线段AC于点Q.设运动时间为t(t>0)秒.
①连接BC,若△BOC与△AMN相似,请直接写出t的值;
②△AOQ能否为等腰三角形?若能,求出t的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是用黑色棋子摆成的美丽图案,按照这样的规律摆下去,第10个这样的图案需要黑色棋子的个数为( )

![]()


A.148B.152C.174D.202
查看答案和解析>>
科目:初中数学 来源: 题型:
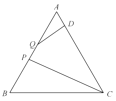
【题目】如图,等边![]() 的边长为3,点
的边长为3,点![]() 在边
在边![]() 上,
上,![]() ,线段
,线段![]() 在边
在边![]() 上运动,
上运动,![]() ,有下列结论:
,有下列结论:
①![]() 与
与![]() 可能相等;②
可能相等;②![]() 与
与![]() 可能相似;③四边形
可能相似;③四边形![]() 面积的最大值为
面积的最大值为![]() ;④四边形
;④四边形![]() 周长的最小值为
周长的最小值为![]() .其中,正确结论的序号为( )
.其中,正确结论的序号为( )
A.①④B.②④C.①③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.

(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
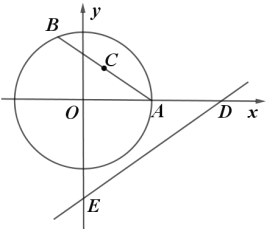
【题目】如图,在平面直角坐标系![]() 中,半径为2的
中,半径为2的![]() 与
与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,点
,点![]() 是
是![]() 上一动点,点
上一动点,点![]() 为弦
为弦![]() 的中点,直线
的中点,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,则
,则![]() 面积的最小值为________.
面积的最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 在平面直角坐标系![]() 中, 点
中, 点![]() 坐标为
坐标为![]() , 点
, 点![]() 在
在![]() 轴正半轴上,直线
轴正半轴上,直线![]() 经过点
经过点![]() 、
、![]() ,且
,且![]() ,
,
(1)若点![]() 的坐标为
的坐标为![]() ,求直线
,求直线![]() 的表达式;
的表达式;
(2)反比例函数![]() 的图像与直线
的图像与直线![]() 交于第一象限的
交于第一象限的![]() 、
、![]() 两点
两点![]() ,当
,当![]() 时,求
时,求![]() 的值(用含
的值(用含![]() 的式子表示);
的式子表示);
(3)在(1)的条件下,设线段![]() 的中点为
的中点为![]() ,过点
,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,交反比例函数
,交反比例函数![]() 的图像于点
的图像于点![]() ,分别连接
,分别连接![]() 、
、![]() , 当
, 当![]() 与
与![]() 相似时,请直接写出满足条件的
相似时,请直接写出满足条件的![]() 值.
值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com