

���� ��1�����츨���ߺ�֤����HGE�ա�CED�����ö�Ӧ�������֤�ı���GHBF�Ǿ��κ����õ��������������FG=CE��FG��CE��
��2�����츨���ߺ�֤����HGE�ա�CED�����ö�Ӧ�������֤�ı���GHBF�Ǿ��κ����õ��������������FG=CE��FG��CE��
��3��֤����CBF�ա�DCE������֤���ı���CEGF��ƽ���ı��Σ����ɵó����ۣ�
��� �⣺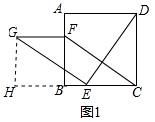 ��1��FG=CE��FG��CE���������£�
��1��FG=CE��FG��CE���������£�
����G��GH��CB���ӳ����ڵ�H����ͼ1��ʾ��
��GH��BF����GHE=90�㣬
��EG��DE��
���GEH+��DEC=90�㣬
�ߡ�GEH+��HGE=90�㣬
���DEC=��HGE��
�ڡ�HGE���CED�У�$\left\{\begin{array}{l}{��GHE=��DCE}&{\;}\\{��HGE=��DEC}&{\;}\\{EG=DE}&{\;}\end{array}\right.$��
���HGE�ա�CED��AAS����
��GH=CE��HE=CD��
��CE=BF��
��GH=BF��
��GH��BF��
���ı���GHBF�Ǿ��Σ�
��GF=BH��FG��CH
��FG��CE��
���ı���ABCD�������Σ�
��CD=BC��
��HE=BC��
��HE+EB=BC+EB��
��BH=EC��
��FG=EC��
�ʴ�Ϊ��FG=CE��FG��CE��
��2��FG=CE��FG��CE��Ȼ�������������£�
����G��GH��CB���ӳ����ڵ�H����ͼ2��ʾ��
��EG��DE��
���GEH+��DEC=90�㣬
�ߡ�GEH+��HGE=90�㣬
���DEC=��HGE��
�ڡ�HGE���CED�У�$\left\{\begin{array}{l}{��GHE=��DCE}&{\;}\\{��HGE=��DEC}&{\;}\\{EG=DE}&{\;}\end{array}\right.$��
���HGE�ա�CED��AAS����
��GH=CE��HE=CD��
��CE=BF����GH=BF��
��GH��BF��
���ı���GHBF�Ǿ��Σ�
��GF=BH��FG��CH
��FG��CE��
���ı���ABCD�������Σ�
��CD=BC��
��HE=BC��
��HE+EB=BC+EB��
��BH=EC��
��FG=EC��
��3��FG=CE��FG��CE��Ȼ�������������£�
���ı���ABCD�������Σ�
��BC=CD����FBC=��ECD=90�㣬
�ڡ�CBF���DCE�У�$\left\{\begin{array}{l}{BF=CE}&{\;}\\{��FBC=��ECD}&{\;}\\{BC=DC}&{\;}\end{array}\right.$��
���CBF�ա�DCE��SAS����
���BCF=��CDE��CF=DE��
��EG=DE����CF=EG��
��DE��EG
���DEC+��CEG=90��
�ߡ�CDE+��DEC=90��
���CDE=��CEG��
���BCF=��CEG��
��CF��EG��
���ı���CEGFƽ���ı��Σ�
��FG��CE��FG=CE��
���� �������ı����ۺ��⣬�����������ε����ʡ�ȫ�������ε��ж������ʡ�ƽ���ı��ε��ж������ʡ����ε��ж������ʵ�֪ʶ�������ۺ���ǿ����һ���Ѷȣ�����Ĺؼ�������ȫ�������εĶ�Ӧ����Ƚ����߶εĵ����������Ӷ���֤��ƽ���ı��Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ʵ��a��b�������ϵĶ�Ӧ���λ����ͼ��ʾ������ȷ�Ľ����ǣ�������
ʵ��a��b�������ϵĶ�Ӧ���λ����ͼ��ʾ������ȷ�Ľ����ǣ�������| A�� | a��-2 | B�� | b��-1 | C�� | -a��-b | D�� | a��|b| |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�ADƽ�֡�BAC����AD���е�O��EF��AD���ֱ�AB��AC�ڵ�E��F������DE��DF��
��ͼ���ڡ�ABC�У�ADƽ�֡�BAC����AD���е�O��EF��AD���ֱ�AB��AC�ڵ�E��F������DE��DF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
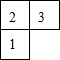 ������ͼ��ʾһ����������ͬС�������ɵļ�����ĸ���ͼ��С�����ε����ֱ�ʾ��λ����С������ĸ�������ü����������ͼΪ��������
������ͼ��ʾһ����������ͬС�������ɵļ�����ĸ���ͼ��С�����ε����ֱ�ʾ��λ����С������ĸ�������ü����������ͼΪ��������| A�� | 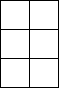 | B�� | 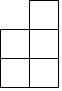 | C�� | 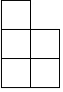 | D�� | 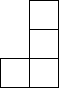 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
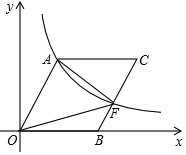 ��ͼ��OΪ����ԭ�㣬��B��x���ϣ��ı���OACBΪƽ���ı��Σ�cos��AOB=$\frac{3}{5}$������������y=$\frac{k}{x}��k��0��$�ڵ�һ�����ڵ�ͼ����A����BC���ڵ�F��
��ͼ��OΪ����ԭ�㣬��B��x���ϣ��ı���OACBΪƽ���ı��Σ�cos��AOB=$\frac{3}{5}$������������y=$\frac{k}{x}��k��0��$�ڵ�һ�����ڵ�ͼ����A����BC���ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
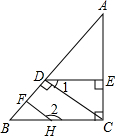 ��ͼ����֪AC��BC��CD��AB��DE��AC����1���2�������ж�HF��AB�Ƿ�ֱ����˵�����ɣ���գ�
��ͼ����֪AC��BC��CD��AB��DE��AC����1���2�������ж�HF��AB�Ƿ�ֱ����˵�����ɣ���գ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x=$\frac{1}{2}$ | B�� | x=$-\frac{1}{2}$ | C�� | x=$\frac{1}{3}$ | D�� | x=-$\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com