
在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为 .

【解析】
试题分析:先求证四边形AFPE是矩形,再根据直线外一点到直线上任一点的距离,垂线段最短,利用相似三角形对应边成比例即可求得AP最短时的长,然后即可求出AM最短时的长.
在△ABC中,AB=6,AC=8,BC=10,
∴∠BAC=90°,
∵PE⊥AB,PF⊥AC,
∴四边形AFPE是矩形,
∴EF=AP.
∵M是EF的中点,
∴AM=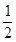 AP,
AP,
根据直线外一点到直线上任一点的距离,垂线段最短,
即AP⊥BC时,AP最短,同样AM也最短,
∴当AP⊥BC时,△ABP∽△CBA,
∴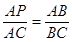 ,
,
∴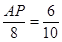 ,
,
∴AP最短时,AP=4.8
∴当AM最短时,AM=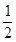 AF=2.4.
AF=2.4.
考点:1.相似三角形判定与性质;2.垂线段最短;3.直角三角形斜边上的中线


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012届浙江省桐乡市河山镇中学学校九年级第一学期期末调研测试数学卷 题型:填空题
如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60º,若BE=6 cm,DE=2cm,则BC=______________.
查看答案和解析>>
科目:初中数学 来源:2013届江苏省无锡市江南中学九年级二模数学试卷(带解析) 题型:解答题
如图,在△ABC中,AB=AC=10cm,BD⊥AC于D,且BD=8cm.点M从点A出发,沿AC方向匀速运动,速度为2cm/s;同时直线PQ由点B出发沿BA方向匀速运动,速度为1cm/s,运动过程中始终保持PQ∥AC,直线PQ交AB于P,交BC于Q,连接PM,设运动时间为t(s)(0<t<5).
(1)当四边形PQCM是平行四边形时,求t的值;
(2)当t为何值时,△PQM是等腰三角形?
(3)以PM为直径作⊙E,在点P、Q整个运动过程中,是否存在这样的时刻t,使得⊙E与BC相切?若存在,请求出运动时间t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省无锡市前洲中学九年级中考模拟考试数学卷 题型:解答题
(本题满分10分)如图1,在△ABC中,AB=BC=5,AC="6." △ECD是△ABC沿BC方向平移得到的,连接AE.AC和BE相交于点O.
(1)判断四边形ABCE是怎样的四边形,说明理由;
(2)如图2,P是线段BC上一动点(图2),(不与点B、C重合),连接PO并延长交线段AE于点Q,QR⊥BD,垂足为点R.
①四边形PQED的面积是否随点P的运动而发生变化?
若变化,请说明理由;若不变,求出四边形PQED的面积;
②当线段BP的长为何值时,△PQR与△BOC相似?
查看答案和解析>>
科目:初中数学 来源:2012届北京市燕山区九年级上学期期末考试数学卷 题型:解答题
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点M、N,在AC的延长线上取点P,使∠CBP=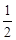 ∠A.
∠A.
【小题1】(1)判断直线BP与⊙O的位置关系,并证明你的结论;
【小题2】(2)若⊙O的半径为1,tan∠CBP=0.5,求BC和BP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com