
分析 (1)根据绘制的频数分布表和频数分布直方图,即可得到家庭人均日用水量在47≤x<51范围的家庭最多,以及这个范围的家庭占全班家庭的百分比;
(2)根据每人每天节约用水8升,按全班50人计算,一年按365天计算,即可得到节约的用水量,按生活基本日均需水量50升的标准计算,即可得到这些水可供1个人生活的时间.
解答 解:计算最大值与最小值的差:62-35=27;
决定组距和组数:取组距为4,由于27÷4=6.75,因此要将整个数据分为7组,
用x(升)表示人均日用水量,则所分的组为:
35≤x<39,39≤x<43,43≤x<47,47≤x<51,51≤x<55,55≤x<59,59≤x<63,
列频数分布表: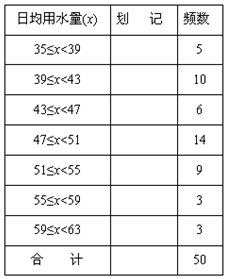
画频数分布直方图: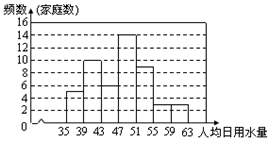
根据频数分布表和频数分布直方图可得:
(1)家庭人均日用水量在47≤x<51范围的家庭最多,
这个范围的家庭占全班家庭的百分比为:$\frac{14}{50}$×100%=28%;
(2)一年(按365天计算)可节约用水:8×50×365÷1000=146(吨),
按生活基本日均需水量50升的标准计算,这些水可供1个人生活:146×1000÷50÷365=8(年).
点评 本题主要考查了频数分布表和频数分布直方图的应用,在统计数据时,经常把数据按照不同的范围分成几个组,分成的组的个数称为组数,每一组两个端点的差称为组距,称这样画出的统计图表为频数分布表.画频率分布直方图的步骤:(1)计算极差.(2)决定组距与组数.(3)确定分点,将数据分组.(4)列频率分布表.(5)绘制频率分布直方图.


 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:解答题
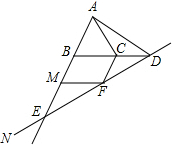 如图,在等边△ABC中,点D在BC的延长线上,连接AD,∠ADN=60°,直线DN交射线AB于点E,过点C作CF∥AB交直线DN于点F,过点F作MF∥BC交射线AB于点M.
如图,在等边△ABC中,点D在BC的延长线上,连接AD,∠ADN=60°,直线DN交射线AB于点E,过点C作CF∥AB交直线DN于点F,过点F作MF∥BC交射线AB于点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
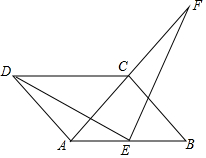 如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上的一点.
如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上的一点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 人员 | 店长 | 厨师甲 | 厨师乙 | 会计 | 服务员甲 | 服务员乙 | 勤杂工 |
| 人数 | 1 | 1 | 1 | 1 | 1 | 3 | 2 |
| 工资额 | 20000 | 7000 | 4000 | 2500 | 2200 | 1800 | 1200 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a3)2=a6 | B. | (-3a2)2=6a4 | C. | (-a2)3=a6 | D. | (-$\frac{1}{2}$ab2)3=$\frac{1}{8}$a3b6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{6-\sqrt{6}}{2}$ | D. | $\frac{6-\sqrt{6}}{2}$或$\frac{6+\sqrt{6}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com