
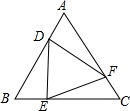
 如图,等边△ABC中,点D,E,F分别同时从点A,B,C出发,以相同的速度在AB,BC,CA上运动,连结DE,EF,DF.
如图,等边△ABC中,点D,E,F分别同时从点A,B,C出发,以相同的速度在AB,BC,CA上运动,连结DE,EF,DF.分析 (1)根据等边三角形的性质得出∠A=∠B=∠C=60°,AB=BC=CA,AD=BE=CF,进一步证得BD=EC=AF,即可证得△ADF≌△BED≌△CFE,根据全等三角形的性质得出DE=EF=FD,即可证得△DEF是等边三角形;
(2)①根据等边三角形得:DE、EF、DF是中位线,由中位线定理得两三角形相似,其相似比为1:2,则面积比为1:4;
②分两种情况:当∠EFC=90°时,如图3,∠FEC=30°,当∠CEF=90°时,如图4,由△ABC和△DEF是等边三角形,得出△DEF∽△ABC,再根据相似三角形的性质即可得出结论.
解答 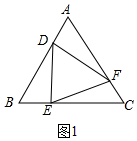 (1)证明:∵△ABC是等边三角形,
(1)证明:∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,AB=BC=CA,
∵AD=BE=CF,
∴BD=EC=AF,
在△ADF、△BED和△CFE中
$\left\{\begin{array}{l}{AD=BE=CF}\\{∠A=∠B=∠C}\\{BD=CE=AF}\end{array}\right.$
∴△ADF≌△BED≌△CFE,
∴DE=EF=FD,
∴△DEF是等边三角形;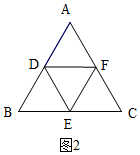
解:(2)有,
①如图2,∵△CEF是等边三角形,
∴EC=FC=EF,
∵AD=BE=CF,
∴D、E、F分别是三边的中点,
∴$\frac{DF}{BC}=\frac{DE}{AC}=\frac{EF}{AB}=\frac{1}{2}$,
∴△DEF∽△BCA,
∴$\frac{{S}_{△DEF}}{{S}_{△ABC}}$=$\frac{1}{4}$;
②∵△ABC和△DEF是等边三角形,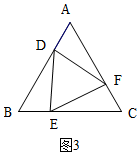
∴△DEF∽△ABC,
当∠EFC=90°时,∠FEC=30°,
∵∠DEF=60°,
∴DE⊥BC,
∴∠BDE=30°,
∴BE=$\frac{1}{2}$BD,即BE=$\frac{1}{3}$BC,CE=$\frac{2}{3}$BC,
∵EF=EC•sin60°=$\frac{2}{3}BC$$•\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{3}BC$,
∴$\frac{{S}_{△DEF}}{{S}_{△ABC}}$=($\frac{EF}{BC}$)2=($\frac{\sqrt{3}}{3}$)2=$\frac{1}{3}$.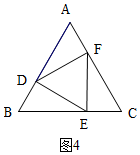
当∠CEF=90°时,如图4,同理可得:$\frac{{S}_{△DEF}}{{S}_{△ABC}}$=($\frac{EF}{BC}$)2=($\frac{\sqrt{3}}{3}$)2=$\frac{1}{3}$.
点评 本题是三角形的综合题,考查的是等边三角形的性质和判定、三角形中位线定理、三角形相似的性质和判定以及动点运动问题,熟知三个动点同时同速度时,路程相等,并知道等边三角形的三个内角都相等,且都等于60°.


科目:初中数学 来源: 题型:选择题
 如图所示,在一块长为22m,宽为17m的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),若剩余部分种上草坪,使草坪的面积为300m2,则所修道路的宽度为( )m.
如图所示,在一块长为22m,宽为17m的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),若剩余部分种上草坪,使草坪的面积为300m2,则所修道路的宽度为( )m.| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 1 | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
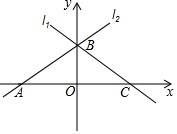 如图,直线l1与直线l2关于y轴对称,已知直线l1的函数表达式为y=-$\frac{4}{3}$x+b,点B 坐标为(0,3),则点A坐标为(-$\frac{9}{4}$,0).
如图,直线l1与直线l2关于y轴对称,已知直线l1的函数表达式为y=-$\frac{4}{3}$x+b,点B 坐标为(0,3),则点A坐标为(-$\frac{9}{4}$,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
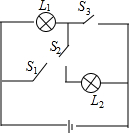 如图所示电路,任意闭合两个开关,能使灯L2亮起来的概率是( )
如图所示电路,任意闭合两个开关,能使灯L2亮起来的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com