
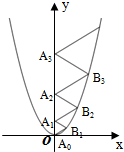
 二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,A1,A2,A3,…,A2016在y轴的正半轴上,B1,B2,B3,…,B2016 在二次函数y=$\frac{2}{3}$x2第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2015B2016A2016都为等边三角形,则△A2015B2016A2016的边长=2016.
二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,A1,A2,A3,…,A2016在y轴的正半轴上,B1,B2,B3,…,B2016 在二次函数y=$\frac{2}{3}$x2第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2015B2016A2016都为等边三角形,则△A2015B2016A2016的边长=2016. 分析 根据等边三角形的性质可得∠A1A0B1=60°,然后表示出A0B1的解析式,与二次函数解析式联立求出点B1的坐标,再根据等边三角形的性质求出A0A1,同理表示出A1B2的解析式,与二次函数解析式联立求出点B2的坐标,再根据等边三角形的性质求出A1A2,同理求出B3的坐标,然后求出A2A3,从而得到等边三角形的边长为从1开始的连续自然数,与三角形所在的序数相等.
解答 解:∵△A0B1A1是等边三角形,
∴∠A1A0B1=60°,
∴A0B1的解析式为y=$\frac{\sqrt{3}}{3}$x,
联立$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{3}x}\\{y=\frac{2}{3}{x}^{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{\sqrt{3}}{2}}\\{y=\frac{1}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$(为原点舍弃)
∴B1($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),
∴等边△A0B1A1的边长为$\frac{1}{2}$×2=1,
同理,A1B2的解析式为y=$\frac{\sqrt{3}}{3}$x+1,
联立$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{3}x+1}\\{y=\frac{2}{3}{x}^{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\sqrt{3}}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{\sqrt{3}}{2}}\\{y=\frac{1}{2}}\end{array}\right.$(在第二象限舍弃)
∴B2($\sqrt{3}$,2),
∴等边△A1B2A2的边长A1A2=2×(2-1)=2,
同理可求出B3($\frac{3\sqrt{3}}{2}$,$\frac{9}{2}$),
所以,等边△A2B3A3的边长A2A3=2×($\frac{9}{2}$-1-2)=3,
…,
以此类推,系列等边三角形的边长为从1开始的连续自然数,
△A2015B2016A2016的边长为2016.
故答案为:2016.
点评 本题考查了二次函数图象上点的坐标特征,等边三角形的性质,主要利用了联立两函数解析式求交点坐标,根据点B系列的坐标求出等边三角形的边长并且发现系列等边三角形的边长为从1开始的连续自然数是解题的关键.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,AE是∠BAC的角平分线,AD是BC边上的高线,且∠B=50°,∠C=60°,则∠EAD的度数( )
如图,△ABC中,AE是∠BAC的角平分线,AD是BC边上的高线,且∠B=50°,∠C=60°,则∠EAD的度数( )| A. | 35° | B. | 5° | C. | 15° | D. | 25° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB是⊙O的直径,弦CD⊥AB于点C,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2.AF=3.给出下列结论:
如图,AB是⊙O的直径,弦CD⊥AB于点C,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2.AF=3.给出下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
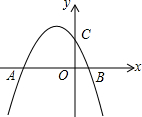 已知抛物线y=-$\frac{1}{2}{x^2}$+bx+c与y轴交于点C,与x轴的两个交点分别为A(-4,0),B(1,0).
已知抛物线y=-$\frac{1}{2}{x^2}$+bx+c与y轴交于点C,与x轴的两个交点分别为A(-4,0),B(1,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
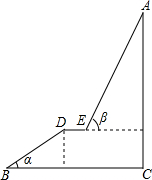 如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,AC=200.4米,BD=100米,∠α=30°,∠β=70°,则AE的长度约为160米.(参考数据:sin70≈0.94,cos70°≈0.34,tan70°≈2.25).
如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,AC=200.4米,BD=100米,∠α=30°,∠β=70°,则AE的长度约为160米.(参考数据:sin70≈0.94,cos70°≈0.34,tan70°≈2.25).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
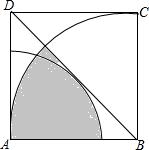 如图所示,以正方形ABCD的顶点A为圆心的弧恰好与对角线BD相切,以顶点B为圆心,正方形的边长为半径的弧,已知正方形的边长为2,则图中阴影部分的面积为( )
如图所示,以正方形ABCD的顶点A为圆心的弧恰好与对角线BD相切,以顶点B为圆心,正方形的边长为半径的弧,已知正方形的边长为2,则图中阴影部分的面积为( )| A. | π-2 | B. | $\frac{π}{2}-1$ | C. | $\frac{5π}{4}-1$ | D. | $\frac{3π}{4}-1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com