练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

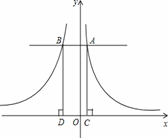
    如图，已知第一象限内的图象是反比例函数y=  图象的一个分支，第二象限内的图象是反比例函数y=-  图象的一个分支，在x轴的上方有一条平行于x轴的直线l与它们分别交于点A、B，过点A、B作x轴的垂线，垂足分别为C、D．若四边形ABCD的周长为8且AB＜AC，则点A的坐标为             

     



    （1/3，3） 

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    随着北京的城市扩张、工业发展和人口膨胀，丰富的地表水系迅速断流、干涸，甚至地下水也超采严重，缺水非常严重. 为了解决水资源紧缺问题，市政府采取了一系列措施. 2014年4月16日北京市发改委公布了两套北京水价调整听证方案，征求民意.

    方案一

    　　第1阶梯：户年用水量不超145立方米，每立方米水价为4.95元

    　　第2阶梯：户年用水量为146-260立方米，每立方米水价为7元

    　　第3阶梯：户年用水量为260立方米以上，每立方米水价为9元

    　　方案二

    　　第1阶梯：户年用水量不超180立方米，每立方米水价为5元

    　　第2阶梯：户年用水量为181-260立方米，每立方米水价为7元

    第3阶梯：户年用水量为260立方米以上，每立方米水价为9元

    例如，若采用方案一，当户年用水量为180立方米时，水费为.

    请根据方案一、二解决以下问题：

    （1）       若采用方案二，当户年水费1040元时，用水量为多少立方米？

    （2）       根据本市居民家庭用水情况调查分析，有93%的居民家庭年用水量在第一阶梯.

    因此我们以户年用水量180立方米为界，即当户年用水量不超过180立方米时，选择哪个方案所缴纳的水费最少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    四边形ABCD中，对角线AC、BD相交于点O，给出下列四个条件： 
    ①AD∥BC；②AD=BC；③OA=OC；④OB=OD                         

    从中任选两个条件，能使四边形ABCD为平行四边形的选法有(  ) 

    A．

    3种

    B．

    4种

    C．

    5种

    D．

    6种

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在正方形ABCD的对角线上取点E，使得∠BAE=15°，连结AE，CE．延长CE到F，连结BF，使得BC=BF．若AB=1，则下列结论：
    ①AE=CE；②F到BC的距离为  ；③BE+EC=EF；④S△AED=     ；⑤S△EBF=   ．
    其中正确的是（　　）

    A．①③         B．①③⑤         C．①②④          D．①③④⑤

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


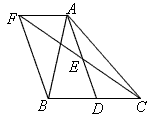
    如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于F ，且AF=BD，连结BF

    （1）求证：D是BC的中点．

    （2）如果AB=AC ，试判断四边形AFBD的形状，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在四边形ABCD中，对角线AC与BD相交于点O，不能判断四边形ABCD是平行四边形的是（　　）

    　  A．AB∥DC，AD=BC B． AB∥DC，AD∥BC  C． AB=DC，AD=BC    D． OA=OC，OB=OD

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    黔东南州某校为了解七年级学生课外学习情况，随机抽取了部分学生作调查，通过调查将获得的数据按性别绘制成如下的女生频数分布表和如图所示的男生频数分布直方图：

    学习时间t（分钟）         人数                      占女生人数百分比

    0≤t＜30                  4                         20%

    30≤t＜60                 m                         15%

    60≤t＜90                 5                         25%

    90≤t＜120                6                         n

    120≤t＜150               2                         10%

    根据图表解答下列问题：

    （1）在女生的频数分布表中，m=　 　，n=　 　．

    （2）此次调查共抽取了多少名学生？

    （3）此次抽样中，学习时间的中位数在哪个时间段？

    （4）从学习时间在120～150分钟的5名学生中依次抽取两名学生调查学习效率，恰好抽到男女生各一名的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若点A（1，y1）和点B（2，y2）在反比例函数y=图象上，则y1与y2的大小关系是：y1　　y2（填“＞”、“＜”或“=”）．

    查看答案和解析>>

    同步练习册答案