
分析 (1)根据根的判别式△=24-8k≥0结合k为正整数即可得出k的值;
(2)根据方程有两个非零的整数根即可得出k的值,将其代入二次函数解析式中再根据平移的性质找出平移后的函数图象的解析式;
(3)根据函数解析式画出函数图象,通过移动直线y=$\frac{1}{2}$x+b图象寻找交点个数与b之间的关系,此题得解.
解答 解:(1)∵方程2x2+4x+k-1=0有实数根,
∴△=42-4×2×(k-1)=24-8k≥0,
∴k≤3.
∵k为正整数,
∴k的值为1,2,3.
(2)∵方程有两个整数根,
∴△=24-8k为正整数的平方数,
∵k=1,2,3,
∴k=1,3.
当k=1时,方程为2x2+4x=0,其中一根为0,
∴k=1舍去;
当k=3时,方程为2x2+4x+2=0,解得:x=-1.
∴关于x的二次函数解析式为y=2x2+4x+2.
根据平移的性质即可得出平移后图象的解析式为y=2x2+4x+2-8=2x2+4x-6.
(3)依照题意画出图形,如图所示.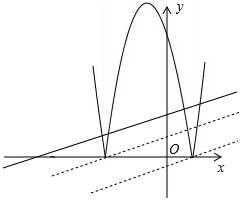
令y=0,则2x2+4x-6=0,
解得:x1=-3,x2=1,
∴该抛物线与x轴的交点坐标为(-3,0)和(1,0).
当点(-3,0)在直线y=$\frac{1}{2}$x+b上时,有0=-$\frac{3}{2}$+b,
解得:b=$\frac{3}{2}$;
当点(1,0)在直线y=$\frac{1}{2}$x+b上时,有0=$\frac{1}{2}$+b,
解得:b=-$\frac{1}{2}$.
结合函数图象可得出:当交点个数为0个时,b<-$\frac{1}{2}$;当交点个数为1个时,b=-$\frac{1}{2}$;当交点个数为2个时,-$\frac{1}{2}$<b<$\frac{3}{2}$;当交点个数为3个时,b=$\frac{3}{2}$;当交点个数为4个时,$\frac{3}{2}$<b<3.
点评 本题考查了根的判别式、平移的性质以及解一元二次方程,根据函数的解析式画出函数图象,利用数形结合解决问题是解题的关键.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
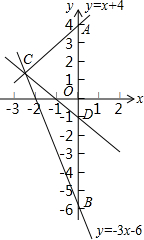 如图所示,设函数y=x+4的图象与y轴交于点A,函数y=-3x-6的图象与y轴交于点B,两个函数的图象交于点C,求通过线段AB的中点D及点C的一次函数表达式.
如图所示,设函数y=x+4的图象与y轴交于点A,函数y=-3x-6的图象与y轴交于点B,两个函数的图象交于点C,求通过线段AB的中点D及点C的一次函数表达式.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 明天一定不下雨 | |
| B. | 一个袋中装有5个红球,从中摸出一个是红球 | |
| C. | 购买1张彩票,中奖 | |
| D. | 随意翻到一本书的某项,这页的页码是奇数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com