练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

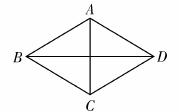
     如图，四边形ABCD的对角线AC、BD互相垂直，则下列条件能判定四边形ABCD为菱形的是（　　）．

    A．BA＝BC                                B．AC、BD互相平分

    C．AC＝BD                                D．AB∥CD


    B【解析】对角线互相垂直平分的四边形为菱形．已知对角线AC、BD互相垂直，则需添加条件：AC、BD互相平分．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    3对    

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知△ABC的三边长分别为17，8，15，则此三角形的面积为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若一组数据3，－1，0，2，x的极差是5，则x＝______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一组数据4，5，6，7，7，8的中位数和众数分别是（　　）．

    A．7，7                B．7，6.5         C．5.5，7          D．6.5，7

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    （1）如图（1），在正方形ABCD中，M是BC边（不含端点B、C）上任意一点，P是BC延长线上一点，N是∠DCP的平分线上一点．若∠AMN＝90°，求证：AM＝MN．下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明．

    证明：在边AB上截取AE＝MC，连接ME．

    正方形ABCD中，∠B＝∠BCD＝90°，AB＝BC．

    ∴　∠NMC＝180°－ ∠AMN－ ∠AMB＝180°－ ∠B－ ∠AMB＝ ∠MAB＝∠MAE．

    （下面请你完成余下的证明过程）

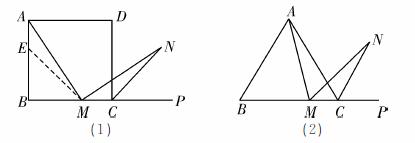
    （2）若将（1）中的“正方形ABCD”改为“正三角形ABC”（如图（2）），N是∠ACP的平分线上一点，则当∠AMN＝60°时，结论AM＝MN是否还成立？请说明理由．

    （3）若将（1）中的“正方形ABCD”改为“正n边形ABCD……X”，请你作出猜想：当∠AMN＝_________°时，结论AM＝MN仍然成立．（直接写出答案，不需要证明）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，AB∥CD，BC∥AD，AE∥CF，则图中全等三角形有（　　）

    　

    A．

    3对

    B．

    4对

    C．

    5对

    D．

    6对

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     方程：x（x+1）=3（x+1）的解的情况是（　　）

    　  A． x=﹣1   B． x=3 C． x1=﹣1，x2=3 D． 以上答案都不对

    查看答案和解析>>

    科目：初中数学 来源： 题型：


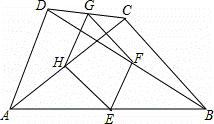
    如图，四边形ABCD中，E、F、G、H分别是AB、BD、CD、AC的中点．

    （1）判断四边形EFGH是何种特殊的四边形，并说明你的理由；

    （2）要使四边形EFGH是菱形，四边形ABCD还应满足的一个条件是　AD=BC　．

    查看答案和解析>>

    同步练习册答案