
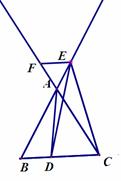
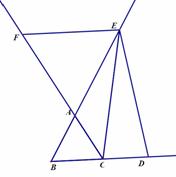
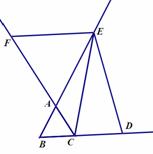
已知:△ABC是正三角形,且边长为1,点E是直线AB上的一个动点,过点E作BC的平行线交直线AC于点F,将线段EC绕点E旋转,使点C落在直线BC上的点D处;
(1)当点E在△ABC的边AB上时,
①求证:AE=BD
②设梯形EDCF的面积为S,当S达到最大值时,求∠ECB的正切值。
(2)当点E不在边AB上时,由A、D、E、C四点围成的四边面积能否为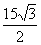 ,若能,求出AE长,若不能请说明理由.
,若能,求出AE长,若不能请说明理由.
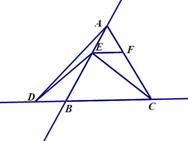
方法一:如图在正ABC中,∠ABC=∠ACB=∠BAC=60o,AB=BC=AC,
∵EF//BC,
∴∠AEF=∠AFE=60o=∠BAC,
∴△AEF是正三角形, ………….1分
 ∴AE=AF=EF,
∴AE=AF=EF,
∴AB-AE=AC-AF,即BE=CF,
又∵∠ABC=∠EDB+∠BED==60o,
∠ACB=∠ECB+∠FCE==60o,
∵ED=EC,
∴∠EDB=∠ECB,
∴∠BED=∠FCE,
∴△EDB≌△CEF………….1分
DB=EF,
∴AE=BD………….1分
方法二: :如图,在正ABC中,∠ABC=∠ACB=60o∠ABD=120o,
又∵∠ABC=∠EDB+∠BED,∠ACB=∠ECB+∠FCE,
∵ED=EC,
∴∠EDB=∠ECB,
∴∠BED=∠FCE,
∵EF//BC, ………….1分
∴∠AEF=∠AFE=60o=∠BAC,
∴△AEF是正三角形, ∠EFC=180o-∠ACB=120o,
∴△EDB≌△CEF………….1分
DB=EF,
∴AE=BD………….1分
第(1)小题②
解答:过点E作EH⊥DC于点H,
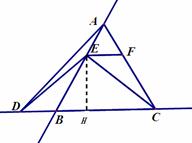 设AE=x,则s=
设AE=x,则s=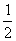 (EF+DC) ×EH=
(EF+DC) ×EH=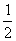 (x+x+1) ×
(x+x+1) ×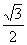 (1-x) ………….1分
(1-x) ………….1分
=-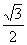 x2+
x2+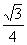 x+
x+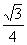
当x=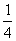 时,有最大值;
时,有最大值;
 此时,EB=
此时,EB=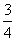 ,则EH=
,则EH=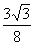 ,BH=
,BH=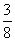 ,CH=
,CH=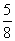 ,………….1分
,………….1分
tan∠ECB=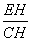 =
= =
=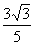 ………….1分
………….1分
第(2)小题分类讨论:当点E在BA延长线上,且AE<1时;当点E在BA延长线上,且AE>1时;当点E在AB延长线上时.共三种情况。
解:当点E不在边AB上时,由A、D、E、C四点围成的四边面积能为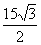 ,具体解答过程如下:
,具体解答过程如下:
设AE=x,分以下三种情况讨论:
 1)当点E在BA延长线上,且AE<1时;由(1)第①同理可得AE=BD,S四边形ADCE=S△BCE-S△BDA=
1)当点E在BA延长线上,且AE<1时;由(1)第①同理可得AE=BD,S四边形ADCE=S△BCE-S△BDA=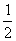 ×BE×BC×sin60o-
×BE×BC×sin60o-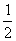 ×BE×BC×sin60o=
×BE×BC×sin60o=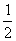 ×(x+1)×1×sin60o-
×(x+1)×1×sin60o-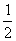 x×1×sin60o=
x×1×sin60o=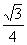 ≠
≠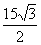 ,不成立…………2分
,不成立…………2分
2) 当点E在BA延长线上,且AE>1时;S四边形AEDC=S△BDE-S△BAC=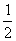 ×BE×BD×sin60o-
×BE×BD×sin60o-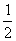 ×BA×BC×sin60o=
×BA×BC×sin60o=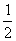 ×(x+1)×x×sin60o-
×(x+1)×x×sin60o-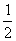 ×1×1×sin60o=
×1×1×sin60o=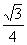 (x2+x-1)
(x2+x-1)
 由题意得:
由题意得: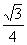 (x2+x-1)=
(x2+x-1)= 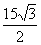
解得:x1=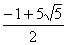 ,x1=
,x1=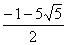 (舍去) ………….2分
(舍去) ………….2分
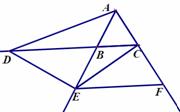 3)当点E在AB延长线上时;S四边形ADECC=S△ADC+S△EDC=
3)当点E在AB延长线上时;S四边形ADECC=S△ADC+S△EDC=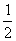 ×DC×AM+
×DC×AM+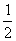 ×DC×EN=
×DC×EN=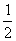 DC×AE×sin60o=
DC×AE×sin60o=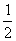 ×(x+1)×x×sin60o=
×(x+1)×x×sin60o=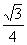 (x2+x)
(x2+x)
得: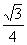 (x2+x)=
(x2+x)= 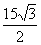
解得:x1=5 ,x2=-6(舍去)
综上所述,当时AE=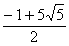 或5时,由A、D、E、C四点围成的四边面积为
或5时,由A、D、E、C四点围成的四边面积为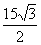 。………….2分
。………….2分


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
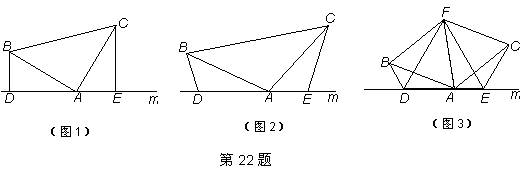
(1)如图(1),在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.易知DE=BD+CE. 若将条件改为:如图(2),在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=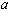 ,其中
,其中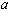 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(2) 拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试推理△DEF的形状. (2013年山东东营第23题改编)
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
某校在七年级设立了六个课外兴趣小组,每个参加者只能参加一个兴趣小组,下面是六个兴趣小组不完整的频数分布直方图和扇形统计图. 根据图中信息,可得下列结论不正确的是( )
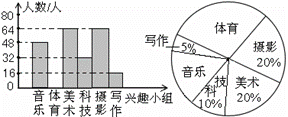 A.七年级共有320人参加了兴趣小组;
A.七年级共有320人参加了兴趣小组;
B.体育兴趣小组对应扇形圆心角的度数为96°;
C.美术兴趣小组对应扇形圆心角的度数为72°;
D.各小组人数组成的数据中位数是56.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com