
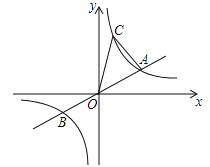
【题目】如图,已知:直线![]() 与双曲线
与双曲线![]() 交于A.B两点,且点A的横坐标为4, 若双曲线
交于A.B两点,且点A的横坐标为4, 若双曲线![]() 上一点C的纵坐标为8,连接AC.
上一点C的纵坐标为8,连接AC.
(1)填空: k的值为_______; 点B的坐标为___________;点C的坐标为___________.
(2)直接写出关于的不等式![]() 的解集.
的解集.
(3)求三角形AOC的面积
(4) 若在x轴上有点M,y轴上有点N,且点M.N.A.C四点恰好构成平行四边形,直接写出点M.N的坐标.
【答案】(1)k=8 ,B(-4,-2),C(1,8) ;(2)![]() ;(3) 15;(4)M(3,0)、N(0,6)或M(-3,0)、N(0,-6)
;(3) 15;(4)M(3,0)、N(0,6)或M(-3,0)、N(0,-6)
【解析】分析:(1)由直线![]() 与双曲线
与双曲线![]() 交于A、B两点,A点横坐标为4,代入正比例函数,可求得点A的坐标,继而求得k值,把C的纵坐标代入反比例函数,即可得到C的坐标;根据对称性,可求得点B的坐标.
交于A、B两点,A点横坐标为4,代入正比例函数,可求得点A的坐标,继而求得k值,把C的纵坐标代入反比例函数,即可得到C的坐标;根据对称性,可求得点B的坐标.
(2)结合图象,即可求得关于x的不等式![]() 的解集;
的解集;
(3)首先过点C作CD⊥x轴于点D,过点A作AE⊥轴于点E,可得S△AOC=S△OCD+S梯形AEDC﹣S△AOE=S梯形AEDC,又由双曲线![]() 上有一点C的纵坐标为8,可求得点C的坐标,继而求得答案;
上有一点C的纵坐标为8,可求得点C的坐标,继而求得答案;
(4)由当MN∥AC,且MN=AC时,点M、N、A、C四点恰好构成平行四边形,根据平移的性质,即可求得答案.
详解:(1)∵直线![]() 与双曲线
与双曲线![]() 交于A、B两点,A点横坐标为4,∴点A的纵坐标为:y=
交于A、B两点,A点横坐标为4,∴点A的纵坐标为:y=![]() ×4=2,∴点A(4,2),∴2=
×4=2,∴点A(4,2),∴2=![]() ,∴k=8,∴
,∴k=8,∴![]() ;把y=8代入
;把y=8代入![]() ,解得:x=1,∴C(1,8).
,解得:x=1,∴C(1,8).
∵直线![]() 与双曲线
与双曲线![]() 交于A、B两点,∴B(﹣4,﹣2);
交于A、B两点,∴B(﹣4,﹣2);
(2)由图象可知:关于x的不等式![]() 的解集为:﹣4≤x<0或x≥4;
的解集为:﹣4≤x<0或x≥4;
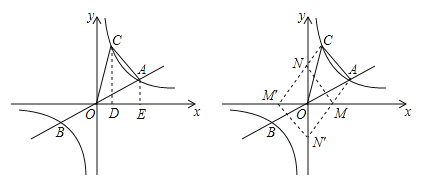
(3)过点C作CD⊥x轴于点D,过点A作AE⊥x轴于点E.
∵双曲线![]() 上有一点C的纵坐标为8,∴把y=8代入y=
上有一点C的纵坐标为8,∴把y=8代入y=![]() ,得:x=1,∴点C(1,8),∴S△AOC=S△OCD+S梯形AEDC﹣S△AOE=S梯形AEDC=
,得:x=1,∴点C(1,8),∴S△AOC=S△OCD+S梯形AEDC﹣S△AOE=S梯形AEDC=![]() ×(2+8)×(4﹣1)=15;
×(2+8)×(4﹣1)=15;
(4)如图,当MN∥AC,且MN=AC时,点M、N、A、C四点恰好构成平行四边形.
∵点A(4,2),点C(1,8),∴根据平移的性质可得:M(3,0),N(0,6)或M′(﹣3,0),N′(0,﹣6).


科目:初中数学 来源: 题型:
【题目】某单位计划用3天时间进行设备检修,安排小王,小李,小赵三位工程师各带班一天,带班顺序是随机确定的.
(1)请你写出三天带班顺序的所有可能的结果;
(2)求小李和小赵恰好相邻的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
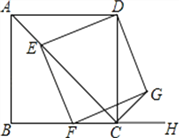
【题目】如图,已知四边形ABCD为正方形,AB=![]() ,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学中,有许多关系都是在不经意间被发现的.当然,没有敏锐的观察力是做不到的.数学家们往往是这样来研究问题的:特值探究–猜想归纳–逻辑证明–总结应用.下面我们也来像数学家们那样分四步找出这两个代数式的关系:对于代数式![]() 与
与![]() .
.
![]() 特值探究:
特值探究:
当![]() ,
,![]() 时,
时,![]() ________;
________;![]() ________
________
当![]() ,
,![]() 时,
时,![]() ________;
________;![]() ________
________
![]() 猜想归纳:
猜想归纳:
观察![]() 的结果,写出
的结果,写出![]() 与
与![]() 的关系:________.
的关系:________.
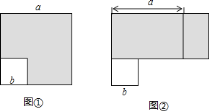
![]() 逻辑证明:如图,边长为
逻辑证明:如图,边长为![]() 的正方形纸片剪出一个边长为
的正方形纸片剪出一个边长为![]() 的小正方形之后,剩余部分(即阴影部分)又剪拼成一个矩形(不重叠无缝隙),请你说说是如何用这个图来得出
的小正方形之后,剩余部分(即阴影部分)又剪拼成一个矩形(不重叠无缝隙),请你说说是如何用这个图来得出![]() 中的关系?
中的关系?
![]() 总结应用:利用你发现的关系,求:
总结应用:利用你发现的关系,求:
①若![]() ,且
,且![]() ,则
,则![]() ________;
________;
②![]() 的值.(提示:你可能要用到公式
的值.(提示:你可能要用到公式![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°.点D是直线BC上的一个动点,连接AD,并以AD为边在AD的右侧作等边△ADE.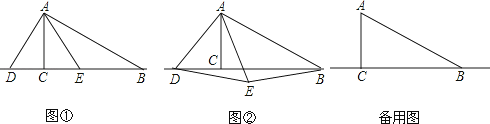
(1)如图①,当点E恰好在线段BC上时,请判断线段DE和BE的数量关系,并结合图①证明你的结论;
(2)当点E不在直线BC上时,连接BE,其它条件不变,(1)中结论是否成立?若成立,请结合图②给予证明;若不成立,请直接写出新的结论;
(3)若AC=3,点D在直线BC上移动的过程中,是否存在以A、C、D、E为顶点的四边形是梯形?如果存在,直接写出线段CD的长度;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线的对称轴是直线x=2,顶点A的纵坐标为1,点B(4,0)在此抛物线上.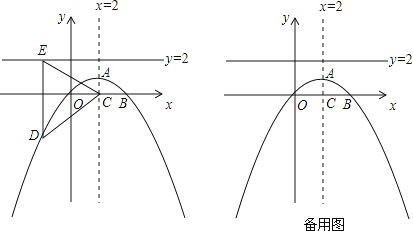
(1)求此抛物线的解析式;
(2)若此抛物线对称轴与x轴交点为C,点D(x,y)为抛物线上一动点,过点D作直线y=2的垂线,垂足为E.
①用含y的代数式表示CD2 , 并猜想CD2与DE2之间的数量关系,请给出证明;
②在此抛物线上是否存在点D,使∠EDC=120°?如果存在,请直接写出D点坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°,②OC=OE,③tan∠OCD= ![]() ,④S△ODC=S四边形BEOF中,正确的有( )
,④S△ODC=S四边形BEOF中,正确的有( ) 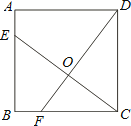
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暴雨过后,某地遭遇山体滑坡,武警总队派出一队武警战士前往抢险.半小时后,第二队前去支援,平均速度是第一队的1.5倍,结果两队同时到达.已知抢险队的出发地与灾区的距离为90千米,两队所行路线相同.
(1)问两队的平均速度分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把三角形按如图所示的规律拼图案,其中第①个图案中有4个三角形,第②个图案中有6个三角形,第③个图案中有8个三角形,…,按此规律排列下去,则第⑦个图案中三角形的个数为( )

A. 12 B. 14 C. 16 D. 18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com