
����Ŀ��һ�����εij�Ϊa����Ϊb(a��0��b��0)������ε����Ϊab.����ʽxy(x��0��y��0)���Կ����DZ߳�Ϊx��y�ľ��ε����.���ǿ����ɴ˽�һԪ���η��̣�x2+x��6��0(x��0).����������£�
�ٷ��̱���Ϊx(x+1)��6.
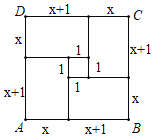
�ڻ��ĸ��߳�Ϊx+1��x�ľ�����ͼ���ã�
���������ϵ��ⷽ��.
��SABCD��(x+x+1)2����SABCD��4x(x+1)+12.
��(x+x+1)2��4x(x+1)+1����x(x+1)��6��
��(2x+1)2��25��
��x��0��
��x��2.
�����������������x�Ķ��η���x2+mx��n��0�Ľ�(x��0��m��0��n��0).(Ҫ����ʾ��ͼ����ע����߶εij��ȣ�д�����ⲽ��)

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��y=kx��k��0�������㣨12����5������ֱ������ƽ��m��m��0������λ����ƽ�ƺ�õ���ֱ����뾶Ϊ6����O�ཻ����OΪ����ԭ�㣩����m��ȡֵ��ΧΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���������ι��ţ�������������ˮλ��AB��20m��ˮλ����3m�ʹﵽ������CD������ˮ�����Ϊ10m��

��1������ͼ������ϵ���������ߵĽ���ʽ��
(2)����ˮ����ʱ��ˮλ��ÿСʱ0.2m���ٶ��������Ӿ����߿�ʼ���ٳ�������Сʱ���ܵ����Ŷ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ϸ���![]() �ſ�Ƭ������ֱ��������
�ſ�Ƭ������ֱ��������![]() ��
��![]() ��
��![]() ��
��![]() ����Щ��Ƭ����������ȫ��ͬ������Щ��Ƭ���泯��ϴ�Ⱥ���������ϣ��״���������һ�ţ����¿�Ƭ�ϵ����ֺ��Է��泯�ϷŻ�ϴ�ȣ���Ҳ����������һ�ţ����¿�Ƭ�ϵ����֣�Ȼ����������ӣ�
����Щ��Ƭ����������ȫ��ͬ������Щ��Ƭ���泯��ϴ�Ⱥ���������ϣ��״���������һ�ţ����¿�Ƭ�ϵ����ֺ��Է��泯�ϷŻ�ϴ�ȣ���Ҳ����������һ�ţ����¿�Ƭ�ϵ����֣�Ȼ����������ӣ�
![]() �����б�����״ͼ�ķ���������֮��Ϊ
�����б�����״ͼ�ķ���������֮��Ϊ![]() �ĸ��ʣ�
�ĸ��ʣ�
![]() �������Ұ�������ʽ����Ϸ��������֮��Ϊ
�������Ұ�������ʽ����Ϸ��������֮��Ϊ![]() ʱ����ʤ��������֮�Ͳ�Ϊ
ʱ����ʤ��������֮�Ͳ�Ϊ![]() ʱ������ʤ������ʤһ�ε�
ʱ������ʤ������ʤһ�ε�![]() �֣�˭�ȴﵽ
�֣�˭�ȴﵽ![]() ��Ϊʤ����ô��ʤһ�εö��ٷ֣������Ϸ��˫����ƽ��
��Ϊʤ����ô��ʤһ�εö��ٷ֣������Ϸ��˫����ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ⱳ������ͼ1�����ı���ABCD��,AB=AD,��BAD=120 ,��B=��ADC=90��.E��F�ֱ��� BC,CD �ϵĵ㡣�ҡ�EAF=60�� . ̽��ͼ���߶�BE��EF��FD ֮���������ϵ�� С��ͬѧ̽��������ķ�����,�ӳ� FD ���� G,ʹ DG=BE,���� AG,��֤����ABE�ա�ADG, ��֤����AEF�ա�AGF���ɵó����ۣ����Ľ���Ӧ��_________��
̽�����죺��ͼ2�����ı���ABCD��,AB=AD,��B+��D=180�� .E,F �ֱ��� BC,CD �ϵĵ�,�ҡ�EAF=![]() ��BAD�����������Ƿ���Ȼ��������˵�����ɣ�
��BAD�����������Ƿ���Ȼ��������˵�����ɣ�
ʵ��Ӧ�ã���ͼ3����ij�ξ�����ϰ�У���ͧ����ָ�����ģ�O������ƫ��30����A��,��ͧ����ָ��������ƫ�� 70����B��,��������ͧ��ָ�����ĵľ������,�ӵ��ж�ָ���,��ͧ��������������55 ����/Сʱ���ٶ�ǰ��,��ͧ���ر�ƫ�� 50���ķ����� 75 ����/Сʱ���ٶ�ǰ��2Сʱ��, ָ�����Ĺ۲�ס�������ͧ�ֱ� E,F ��,������֮ͧ��ļн�Ϊ70�� �������ʱ���� ֮ͧ��ľ��롣

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�İ뾶OD����AB�ڵ�C������AO���ӳ�����O�ڵ�E������EC.��AB=8��CD=2����EC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڸ�����һ��ƽ���ı���ֽƬ����һ�����Σ��ס������˵��������£�
�ף�����AC����AC�Ĵ�ֱƽ����MN�ֱ�AD��AC��BC��M��O��N������AN��CM�����ı���ANCM�����Σ�
�ң��ֱ�����A����B��ƽ����AE��BF���ֱ�BC��AD��E��F������EF�����ı���ABEF�����Σ�
�������˵��������ж�

A������ȷ���Ҵ��� B������ȷ���״��� C���ס��Ҿ���ȷ D���ס��Ҿ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ijС��Ҫ�����Χ��һ���λ�̳����̳��һ�����㹻����ǽ�������������õ����֮��ǡ��Ϊ![]() �ף�
�ף�
��1�������![]() ���������
���������![]() ��ʾ����λ��ƽ���ף����
��ʾ����λ��ƽ���ף����![]() ����
����![]() ��ʾ����λ���ף�֮��ĺ�����ϵʽ����Ҫ��д���Ա���
��ʾ����λ���ף�֮��ĺ�����ϵʽ����Ҫ��д���Ա���![]() ��ȡֵ��Χ��������Χ����ʹ��̳������
��ȡֵ��Χ��������Χ����ʹ��̳������
��2�����Χ����ʹ�˾��λ�̳�����![]() ƽ���ף�
ƽ���ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A=��B=90����E��AB�ϵ�һ�㣬��AE=BC����1=��2��

��1��Rt��ADE��Rt��BECȫ���𣿲�˵�����ɣ�
��2����CDE�Dz���ֱ�������Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com