
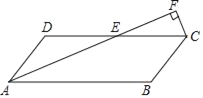
【题目】如图,四边形ABCD为平行四边形,AD=1,AB=3,∠DAB=60°,点E为边CD上一动点,过点C作AE的垂线交AE的延长线于点F.
(1)求∠D的度数;
(2)若点E为CD的中点,求EF的值;
(3)当点E在线段CD上运动时,![]() 是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
【答案】(1)∠ADC=120°;(2)EF=![]() ,(3)有最大值,最大值为:
,(3)有最大值,最大值为:![]()
【解析】
(1)由四边形ABCD是平行四边形,得AB∥CB,进而即可得到答案;
(2)作AH⊥CD交CD的延长线于H,由在Rt△ADH中,∠H=90°,∠ADH=60°,得A=![]() ,DH=
,DH=![]() ,结合勾股定理得AE=
,结合勾股定理得AE=![]() ,易证△AEH∽△CEF,得
,易证△AEH∽△CEF,得![]() ,进而即可求解;
,进而即可求解;
(3)作△AFC的外接圆⊙O,作AH⊥CD交CD的延长线于H,作OK⊥CD于K,交⊙O于M,作FP∥CD交AD的延长线于P,作MN∥CD交AD的延长线于N,作NQ⊥CD于Q.易得PA的值最大时,![]() 的值最大,PA的值最大=AN的长,根据勾股定理和三角函数的定义得DN=
的值最大,PA的值最大=AN的长,根据勾股定理和三角函数的定义得DN=![]() ,从而得AN=AD+DN=
,从而得AN=AD+DN=![]() ,进而即可得到答案.
,进而即可得到答案.
(1)∵四边形ABCD是平行四边形,
∴AB∥CB,
∴∠ADC+∠DAB=180°,
∵∠DAB=60°,
∴∠ADC=120°.
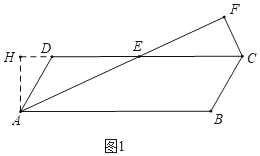
(2)作AH⊥CD交CD的延长线于H,如图1,
∵在Rt△ADH中,∠H=90°,∠ADH=60°,AD=2,
∴AH=ADsin60°=![]() ,DH=ADcos60°=
,DH=ADcos60°=![]() ,
,
∵DE=EC=![]() ,
,
∴EH=DH+DE=2,
∴AE=![]() ,
,
∵CF⊥AF,
∴∠F=∠H=90°,
∵∠AEH=∠CEF,
∴△AEH∽△CEF,
∴![]() ,
,
∴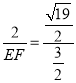 ,
,
∴EF=![]() .
.
(3)如图2中,作△AFC的外接圆⊙O,作AH⊥CD交CD的延长线于H,作OK⊥CD于K,交⊙O于M,作FP∥CD交AD的延长线于P,作MN∥CD交AD的延长线于N,作NQ⊥CD于Q.
∵DE∥PF,
∴![]() ,
,
∵AD是定值,
∴PA的值最大时,![]() 的值最大,
的值最大,
观察图形可知,当点F与点M重合时,PA的值最大,最大值=AN的长,
由(2)可知,AH=![]() ,CH=
,CH=![]() ,∠H=90°,
,∠H=90°,
∴AC=![]() ,
,
∴OM=![]() AC=
AC=![]() ,
,
∵OK∥AH,AO=OC,
∴KH=KC,
∴OK=![]() =
=![]() ,
,
∴MK=NQ=![]() ﹣
﹣![]() ,
,
在Rt△NDQ中,DN= ,
,
∴AN=AD+DN=![]() ,
,
∴![]() 的最大值=
的最大值=![]() =
=![]() .
.



 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是AB边上一点(不与A,B两点重合),下列条件:①∠ACD=∠B; ②∠ADC=∠ACB;③AC2=ADAB;④![]() ,能使△ABC∽△ACD的条件的个数为( )
,能使△ABC∽△ACD的条件的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在平行四边形ABCD中,E为BC边上一点,连结AE、BD且AE=AB

(1)求证:∠ABE=∠EAD;
(2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为上标保障我国海外维和部队官兵的生活,现需通过A港口、B港口分别运送100吨和50吨生活物资.已知该物资在甲仓库存有80吨,乙仓库存有70吨,若从甲、乙两仓库运送物资到港口的费用(元/吨)如表所示:

(1)设从甲仓库运送到A港口的物资为x吨,求总运费y(元)与x(吨)之间的函数关系式,并写出x的取值范围;
(2)求出最低费用,并说明费用最低时的调配方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
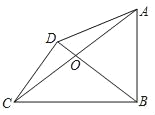
【题目】如图,在四边形ABCD中,∠ABC=90°,对角线AC、BD交于点O,AO=CO,CD⊥BD,如果CD=3,BC=5,那么AB=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2+bx的对称轴为x=1,若关于x的一元二次方程x2+bx﹣t=0(为实数)在﹣1<x<4的范围内有解,则t的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如果某点的横坐标与纵坐标的和为10,则称此点为“合适点”例如,点(1,9),(﹣2019,2029)…都是“合适点”.
(1)求函数y=2x+1的图象上的“合适点”的坐标;
(2)求二次函数y=x2﹣5x﹣2的图象上的两个“合适点”A,B之间线段的长;
(3)若二次函数y=ax2+4x+c的图象上有且只有一个合适点”,其坐标为(4,6),求二次函数y=ax2+4x+c的表达式;
(4)我们将抛物线y=2(x﹣n)2﹣3在x轴下方的图象记为G1,在x轴及x轴上方图象记为G2,现将G1沿x轴向上翻折得到G3,图象G2和图象G3两部分组成的记为G,当图象G上恰有两个“合适点”时,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
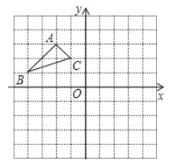
【题目】如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-2,3),B(-4,1),C(-1,2).
(1)画出以点O为旋转中心,将△ABC顺时针旋转90°得到△A'B'C'
(2)求点C在旋转过程中所经过的路径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在△ABC的边AC上,要判断△ADB与△ABC相似,添加一个条件,不正确的是( )
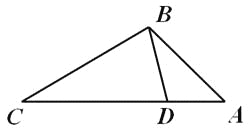
A.∠ABD=∠CB.∠ADB=∠ABCC.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com