
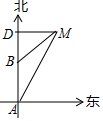
 如图所示,轮船由A处以每小时28海里的速度向正北方向航行,此时测得灯塔M在北偏东30°的方向上(即∠BAM=30°).半小时后,轮船航行到B处,此时测得灯塔M在北偏东60°的方向(即∠DBM=60°).
如图所示,轮船由A处以每小时28海里的速度向正北方向航行,此时测得灯塔M在北偏东30°的方向上(即∠BAM=30°).半小时后,轮船航行到B处,此时测得灯塔M在北偏东60°的方向(即∠DBM=60°).分析 (1)由题意得,AB=28×0.5=14,∠BAM=30°,∠DBM=60°,根据三角形外角的性质得到∠BMA=∠DBM-∠BAM=30°,根据等腰三角形的判定即可得到结论;
(2)由题意得到轮船到达D距离灯塔M最近,列式即可得到结论;
(3)根据三角函数的定义得到DM=7$\sqrt{3}$,根据勾股定理得到CM=$\sqrt{D{C}^{2}+D{M}^{2}}$=7$\sqrt{2}$海里,根据等腰直角三角形的性质即可得到结论.
解答 解:(1)由题意得,AB=28×0.5=14,∠BAM=30°,∠DBM=60°,
∴∠BMA=∠DBM-∠BAM=30°,
∴BM=AB=14,
∴此时轮船与灯塔M的距离是14海里;
(2)∵MD⊥AD,
∴轮船到达D距离灯塔M最近,
∵AD=21,
∴AD-AB=7,
∵7÷28=$\frac{1}{4}$,
∴经过$\frac{1}{4}$小时轮船距离灯塔M最近;
(3)∵∠ADM=90°,
∴$\frac{DM}{AD}$=$\frac{\sqrt{3}}{3}$,
∵AD=21,
∴DM=7$\sqrt{3}$,
∵BC=28×0.5=14,
∴DC=7,
∴CM=$\sqrt{D{C}^{2}+D{M}^{2}}$=7$\sqrt{2}$海里,
∴此时轮船与灯塔M的距离是7$\sqrt{2}$海里;
∵DM=DC,
∴∠DCM=45°,
∴灯塔M在轮船的东南方向上.
点评 本题考查了解直角三角形的应用-方向角问题,三角形外角的性质,等腰三角形的判定,正确理解方向角的定义是解题的关键.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
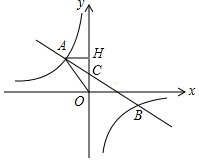 如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于第二、四象限内的A、B两点,与y轴交于C点,过A作AH⊥y轴于H,OH=3,tan∠AOH=$\frac{4}{3}$,点B的坐标为(m,-2).
如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于第二、四象限内的A、B两点,与y轴交于C点,过A作AH⊥y轴于H,OH=3,tan∠AOH=$\frac{4}{3}$,点B的坐标为(m,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com