
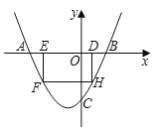
【题目】如图,二次函数![]() 与x轴交于A、B两点,与y轴交于点C,点D与点C关于x轴对称,点P从A点出发向点D运动,点Q在DB上,且∠PCQ=45°,则封闭图形DPCQ(阴影部分)面积的变化情况是( )
与x轴交于A、B两点,与y轴交于点C,点D与点C关于x轴对称,点P从A点出发向点D运动,点Q在DB上,且∠PCQ=45°,则封闭图形DPCQ(阴影部分)面积的变化情况是( )
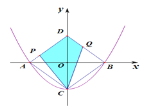
A.一直变大B.始终不变C.先增大后减少D.先减少后增大
【答案】C
【解析】
先证明四边形ABCD是正方形,将△ACP绕点C旋转90°,得到△CAP≌△CBP’进而证得△CPQ≌△CP’Q,得到PQ=PQ’,CB=CH=CA,故△CHP≌△CAP,△CHQ≌△CBQ,得到PH=PA,QH=QB,故S四边形CPDQ=S正方形ABCD-S△CAP-S△CBQ=S正方形ABCD-S△CQP’,当点P是AD中点时,PQ最短,当QP’最短时,△CQP’的面积最小,此时四边形CPDQ的面积最大,故可得到四边形CPDQ的面积先增大后减小.
如图,令![]() =0,解得x1=-2,x2=2,
=0,解得x1=-2,x2=2,
∴A(-2,0), B(2,0),
令x=0,解得y=-2
∴C(0,-2)
故D(0,2)
∴AO=BO=CO=DO,AB⊥CD
则四边形ABCD是正方形,
将△ACP绕点C旋转90°,过C点作CH⊥QP于H点,
∴△CAP≌△CBP’
∴∠PCP’=∠PCB+∠BCP’=∠PCB+∠ACP =90°
∵∠PCQ=45°,
∴∠P’CQ=45°,又CQ=CQ,CP=CP’
∴△CPQ≌△CP’Q
∴PQ=PQ’,
∵CH⊥PQ,CB⊥QP’
∴CB=CH=CA,
又CP=CP
∴△CHP≌△CAP(HL),△CHQ≌△CBQ(HL),
∴PH=PA,QH=QB
故S四边形CPDQ=S正方形ABCD-S△CAP-S△CBQ=S正方形ABCD-S△CQP’
当点P是AD中点时,PQ最短,即QP’最短时,△CQP’的面积最小,
此时四边形CPDQ的面积最大,
故可得到四边形CPDQ的面积先增大后减小.
故选C.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】九龙坡区某社区开展全民读书活动,以丰富人们业余文化生活现计划筹资30000元用于购买科普书籍和文艺刊物
(1)计划购买文艺刊物的资金不少于购买科普书籍资金的2倍,那么最少用多少资金购买文艺刊物?
(2)经初步了解,有200户居民自愿参与集资,那么平均每户需集资150元.经筹委会进步宣传,自愿参加的户数在200户的基础上增加了a%(其中a>50),如果每户平均集资在150元的基础上减少![]() a%,那么实际筹资将比计划筹资多6000元,求a的值.
a%,那么实际筹资将比计划筹资多6000元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成(1)-(3)题.
数学课上,老师出示了这样一道题:
如图,△ABC中,D为BC中点,且AD=AC,M为AD中点,连结CM并延长交AB于N.
探究线段AN、MN、CN之间的数量关系,并证明.
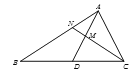
同学们经过思考后,交流了自已的想法:
小明:“通过观察和度量,发现线段AN、AB之间存在某种数量关系.”
小强:“通过倍长不同的中线,可以得到不同的结论,但都是正确的,大家就大胆的探究吧.”
小伟:“通过构造、证明相似三角形、全等三角形,就可以将问题解决.”
......
老师: “若其他条件不变,设AB=a,则可以用含a的式子表示出线段CM的长.”
(1)探究线段AN、AB之间的数量关系,并证明;
(2)探究线段AN、MN、CN之间的数量关系,并证明;
(3)设AB=a,求线段CM的长(用含a的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实国务院的指示精神,地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:![]() . 设这种产品每天的销售利润为w元.
. 设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系内,已知A(2,3),B(4,1),直线l过P(m,0),A、B关于l的对称点分别为A’、B’,请利用直尺(无刻度)和圆规按下列要求作图.
(1)当A’与B重合时,请在图1中画出点P位置,并求出m的值;
(2)当A’、B’都落在y轴上时,请在图2中画出直线l,并求出m的值.
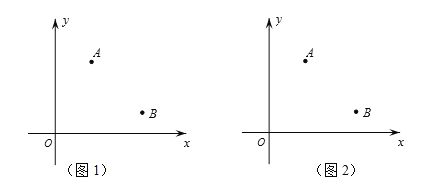
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴相交于点A、B,且过点C(4,3).
轴相交于点A、B,且过点C(4,3).
(1)求![]() 的值和该抛物线顶点P的坐标;
的值和该抛物线顶点P的坐标;
(2)将该抛物线向左平移,记平移后抛物线的顶点为P′,当四边形AP′PB为平行四边形时,求平移后抛物线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象经过点A(1,2)和B(0,-1)且对称轴为x2.
(1)求这个二次函数的解析式;
(2)抛物线上点P(2,m)在图象上,求△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个木制正方体的表面涂上颜色,然后将正方体分割成64个大小相同的小正方体.从这些小正方体中任意取出一个,求取出的小正方体:
(1)三面涂有颜色的概率;
(2)两面涂有颜色的概率;
(3)各个面都没有颜色的概率.
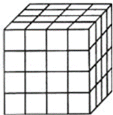
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与 x 轴交于点 A、B,与 y 轴交于点 C,且 OC=2OB, 点 D 为线段 OB 上一动点(不与点 B 重合),过点 D 作矩形 DEFH,点 H、F 在抛物线上,点 E 在 x 轴 上.
与 x 轴交于点 A、B,与 y 轴交于点 C,且 OC=2OB, 点 D 为线段 OB 上一动点(不与点 B 重合),过点 D 作矩形 DEFH,点 H、F 在抛物线上,点 E 在 x 轴 上.
(1)求抛物线的解析式;
(2)当矩形 DEFH 的周长最大时,求矩形 DEFH 的面积;
(3)在(2)的条件下,矩形 DEFH 不动,将抛物线沿着 x 轴向左平移 m 个单位,抛物线与矩形 DEFH的边交于点 M、N,连接 M、N.若 MN 恰好平分矩形 DEFH 的面积,求 m 的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com