
”¾ĢāÄæ”æČēĶ¼£¬Õż·½ŠĪOABCµÄ±ßOA£¬OCŌŚ×ų±źÖįÉĻ£¬µćBµÄ×ų±źĪŖ£Ø©4£¬4£©£®µćP“ÓµćA³ö·¢£¬ŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲxÖįĻņµćOŌĖ¶Æ£»µćQ“ÓµćOĶ¬Ź±³ö·¢£¬ŅŌĻąĶ¬µÄĖŁ¶ČŃŲxÖįµÄÕż·½ĻņŌĖ¶Æ£¬¹ę¶ØµćPµ½“ļµćOŹ±£¬µćQŅ²Ķ£Ö¹ŌĖ¶Æ£®Į¬½ÓBP£¬¹żPµć×÷BPµÄ“¹Ļߣ¬Óė¹żµćQĘ½ŠŠÓŚyÖįµÄÖ±ĻßlĻą½»ÓŚµćD£®BDÓėyÖį½»ÓŚµćE£¬Į¬½ÓPE£®ÉčµćPŌĖ¶ÆµÄŹ±¼äĪŖt£Øs£©£® 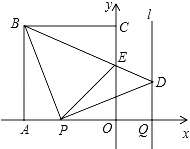
£Ø1£©”ĻPBDµÄ¶ČŹżĪŖ £¬ µćDµÄ×ų±źĪŖ£ØÓĆt±ķŹ¾£©£»
£Ø2£©µ±tĪŖŗĪÖµŹ±£¬”÷PBEĪŖµČŃüČż½ĒŠĪ£æ
£Ø3£©Ģ½Ė÷”÷POEÖܳ¤ŹĒ·ńĖꏱ¼ätµÄ±ä»Æ¶ų±ä»Æ£æČō±ä»Æ£¬ĖµĆ÷ĄķÓÉ£»Čō²»±ä£¬ŹŌĒóÕāøö¶ØÖµ£®
”¾“š°ø”æ
£Ø1£©½ā£ŗ45”ć£»£Øt£¬t£©
£Ø2£©½ā£ŗ¢ŁČōPB=PE£¬
ÓÉ”÷PAB”Õ”÷DQPµĆPB=PD£¬
ĻŌČ»PB”ŁPE£¬
”ąÕāÖÖĒéæöÓ¦ÉįČ„£®
¢ŚČōEB=EP£¬
Ōņ”ĻPBE=”ĻBPE=45”ć£®
”ą”ĻBEP=90”ć£®
”ą”ĻPEO=90”ć©”ĻBEC=”ĻEBC£®
ŌŚ”÷POEŗĶ”÷ECBÖŠ£¬
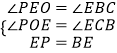
”ą”÷POE”Õ”÷ECB£ØAAS£©£®
”ąOE=CB=OC£®
”ąµćEÓėµćCÖŲŗĻ£ØEC=0£©£®
”ąµćPÓėµćOÖŲŗĻ£ØPO=0£©£®
”ßµćB£Ø©4£¬4£©£¬
”ąAO=CO=4£®
“ĖŹ±t=AP=AO=4£®
¢ŪČōBP=BE£¬
ŌŚRt”÷BAPŗĶRt”÷BCEÖŠ£¬
![]()
”ąRt”÷BAP”ÕRt”÷BCE£ØHL£©£®
”ąAP=CE£®
”ßAP=t£¬
”ąCE=t£®
”ąPO=EO=4©t£®
”ß”ĻPOE=90”ć£¬
”ąPE= ![]()
= ![]() £Ø4©t£©£®
£Ø4©t£©£®
ŃÓ³¤OAµ½µćF£¬Ź¹µĆAF=CE£¬Į¬½ÓBF£¬ČēĶ¼2ĖłŹ¾£®
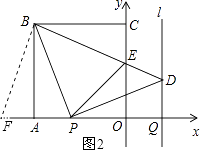
ŌŚ”÷FABŗĶ”÷ECBÖŠ£¬
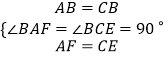
”ą”÷FAB”Õ”÷ECB£®
”ąFB=EB£¬”ĻFBA=”ĻEBC£®
”ß”ĻEBP=45”ć£¬”ĻABC=90”ć£¬
”ą”ĻABP+”ĻEBC=45”ć£®
”ą”ĻFBP=”ĻFBA+”ĻABP
=”ĻEBC+”ĻABP=45”ć£®
”ą”ĻFBP=”ĻEBP£®
ŌŚ”÷FBPŗĶ”÷EBPÖŠ£¬
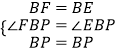
”ą”÷FBP”Õ”÷EBP£ØSAS£©£®
”ąFP=EP£®
”ąEP=FP=FA+AP
=CE+AP£®
”ąEP=t+t=2t£®
”ą ![]() £Ø4©t£©=2t£®
£Ø4©t£©=2t£®
½āµĆ£ŗt=4 ![]() ©4
©4
”ąµ±tĪŖ4Ćė»ņ£Ø4 ![]() ©4£©ĆėŹ±£¬”÷PBEĪŖµČŃüČż½ĒŠĪ
©4£©ĆėŹ±£¬”÷PBEĪŖµČŃüČż½ĒŠĪ
£Ø3£©½ā£ŗ”ßEP=CE+AP£¬
”ąOP+PE+OE=OP+AP+CE+OE
=AO+CO
=4+4
=8£®
”ą”÷POEÖܳ¤ŹĒ¶ØÖµ£¬øƶØÖµĪŖ8
”¾½āĪö”æ½ā£ŗ£Ø1£©ČēĶ¼1£¬ 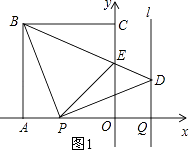
ÓÉĢāæÉµĆ£ŗAP=OQ=1”Įt=t£ØĆė£©
”ąAO=PQ£®
”ßĖıߊĪOABCŹĒÕż·½ŠĪ£¬
”ąAO=AB=BC=OC£¬
”ĻBAO=”ĻAOC=”ĻOCB=”ĻABC=90”ć£®
”ßDP”ĶBP£¬
”ą”ĻBPD=90”ć£®
”ą”ĻBPA=90”ć©”ĻDPQ=”ĻPDQ£®
”ßAO=PQ£¬AO=AB£¬
”ąAB=PQ£®
ŌŚ”÷BAPŗĶ”÷PQDÖŠ£¬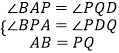
”ą”÷BAP”Õ”÷PQD£ØAAS£©£®
”ąAP=QD£¬BP=PD£®
”ß”ĻBPD=90”ć£¬BP=PD£¬
”ą”ĻPBD=”ĻPDB=45”ć£®
”ßAP=t£¬
”ąDQ=t£®
”ąµćD×ų±źĪŖ£Øt£¬t£©£®
¹Ź“š°øĪŖ£ŗ45”ć£¬£Øt£¬t£©£®
£Ø1£©Ņ×Ö¤”÷BAP”Õ”÷PQD£¬“Ó¶ųµĆµ½DQ=AP=t£¬“Ó¶ųæÉŅŌĒó³ö”ĻPBDµÄ¶ČŹżŗĶµćDµÄ×ų±ź£®£Ø2£©ÓÉÓŚ”ĻEBP=45”ć£¬¹ŹĶ¼1ŹĒŅŌÕż·½ŠĪĪŖ±³¾°µÄŅ»øö»ł±¾Ķ¼ŠĪ£¬ČŻŅ׵Ƶ½EP=AP+CE£®ÓÉÓŚ”÷PBEµ×±ß²»¶Ø£¬¹Ź·ÖČżÖÖĒéæöĢÖĀŪ£¬½čÖśÓŚČż½ĒŠĪČ«µČ¼°¹“¹É¶ØĄķ½ųŠŠĒó½ā£¬Č»ŗó½įŗĻĢõ¼ž½ųŠŠČ”Éį£¬×īÖÕČ·¶Ø·ūŗĻŅŖĒóµÄtÖµ£®£Ø3£©ÓÉ£Ø2£©ŅŃÖ¤µÄ½įĀŪEP=AP+CEŗÜČŻŅ׵Ƶ½”÷POEÖܳ¤µČÓŚAO+CO=8£¬“Ó¶ų½ā¾öĪŹĢā£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
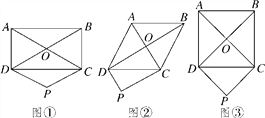
”¾ĢāÄæ”æČēĶ¼¢Ł£¬¾ŲŠĪABCDµÄ¶Ō½ĒĻßAC£¬BD½»ÓŚµćO£¬¹żµćD×÷DP”ĪOC£¬ĒŅDP£½OC£¬Į¬½ÓCP.
(1)ÅŠ¶ĻĖıߊĪCODPµÄŠĪד²¢ĖµĆ÷ĄķÓÉ£»
(2)ČēĶ¼¢Ś£¬Čē¹ūĢāÄæÖŠµÄ¾ŲŠĪ±äĪŖĮāŠĪ£¬ÅŠ¶ĻĖıߊĪCODPµÄŠĪד²¢ĖµĆ÷ĄķÓÉ£»
(3)ČēĶ¼¢Ū£¬Čē¹ūĢāÄæÖŠµÄ¾ŲŠĪ±äĪŖÕż·½ŠĪ£¬ÅŠ¶ĻĖıߊĪCODPµÄŠĪד²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌĶĮ²ÄĮĻ£ŗ
¶ŌÓŚĻ߶ĪµÄ“¹Ö±Ę½·ÖĻßĪŅĆĒÓŠČēĻĀ½įĀŪ£ŗµ½Ļ߶ĪĮ½øö¶Ėµć¾ąĄėĻąµČµÄµćŌŚĻ߶ĪµÄ“¹Ö±Ę½·ÖĻßÉĻ£®¼“ČēĶ¼¢Ł£¬ČōPA£½PB£¬ŌņµćPŌŚĻ߶ĪABµÄ“¹Ö±Ę½·ÖĻßÉĻ£®

Ēėøł¾ŻŌĶĮ²ÄĮĻ£¬½ā¾öĻĀĮŠĪŹĢā£ŗ
ČēĶ¼¢Ś£¬Ö±ĻßCDŹĒµČ±ß”÷ABCµÄ¶Ō³ĘÖį£¬µćDŌŚABÉĻ£¬µćEŹĒĻ߶ĪCDÉĻµÄŅ»¶Æµć£ØµćE²»ÓėµćC”¢DÖŲŗĻ£©£¬Į¬½įAE”¢BE£¬”÷ABE¾Ė³Ź±ÕėŠż×ŖŗóÓė”÷BCFÖŲŗĻ£®
£Ø1£©Šż×ŖÖŠŠÄŹĒµć”” ””£¬Šż×ŖĮĖ”” ””£Ø¶Č£©£»
£Ø2£©µ±µćE“ÓµćDĻņµćCŅĘ¶ÆŹ±£¬Į¬½įAF£¬ÉčAFÓėCD½»ÓŚµćP£¬ŌŚĶ¼¢ŚÖŠ½«Ķ¼ŠĪ²¹Č«£¬²¢Ģ½¾æ”ĻAPCµÄ“󊔏Ē·ń±£³Ö²»±ä£æČō²»±ä£¬ĒėĒó³ö”ĻAPCµÄ¶ČŹż£»Čōøı䣬ĒėĖµ³ö±ä»ÆĒéæö£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĮĖ½āѧɜĢåӿѵĮ·µÄĒéæö£¬Ä³ŹŠ“ÓČ«ŹŠ¾ÅÄź¼¶Ń§ÉśÖŠĖ껜³éČ”²æ·Öѧɜ½ųŠŠĮĖŅ»“ĪĢåÓżæĘÄæ²āŹŌ£Ø°Ń³É¼Ø½į¹ū·ÖĪŖĖÄøöµČ¼¶£ŗA¼¶£ŗÓÅŠć£»B¼¶£ŗĮ¼ŗĆ£»C¼¶£ŗ¼°øń£»D¼¶£ŗ²»¼°øń£©£¬²¢½«²āŹŌ½į¹ū»ę³ÉĮĖČēĻĀĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼£®Ēėøł¾ŻĶ³¼ĘĶ¼ÖŠµÄŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ 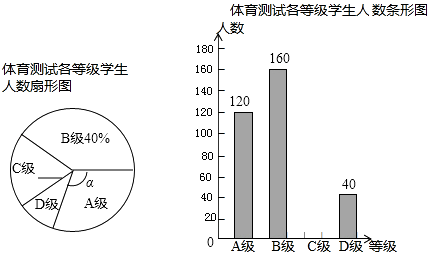
£Ø1£©Ē󱾓Ī³éŃł²āŹŌµÄѧɜČĖŹż£»
£Ø2£©ĒóÉČŠĪĶ¼ÖŠ”Ļ¦ĮµÄ¶ČŹż£¬²¢°ŃĢõŠĪĶ³¼ĘĶ¼²¹³äĶźÕū£»
£Ø3£©øĆŹŠ¾ÅÄź¼¶¹²ÓŠŃ§Éś9000Ćū£¬Čē¹ūČ«²æ²Ī¼ÓÕā“ĪĢåÓż²āŹŌ£¬Ōņ²āŹŌµČ¼¶ĪŖDµÄŌ¼ÓŠ¶ąÉŁČĖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼¢Ł£¬ŌŚ¾ŲŠĪABCDÖŠ£¬AB£½10 cm£¬BC£½8 cm.µćP“ÓµćA³ö·¢£¬ŃŲA”śB”śC”śDµÄĀ·ĻßŌĖ¶Æ£¬µ½µćDĶ£Ö¹£»µćQ“ÓµćD³ö·¢£¬ŃŲD”śC”śB”śAµÄĀ·ĻßŌĖ¶Æ£¬µ½µćAĶ£Ö¹£®ČōµćP”¢µćQĶ¬Ź±³ö·¢£¬µćPµÄĖŁ¶ČĪŖĆæĆė1 cm£¬µćQµÄĖŁ¶ČĪŖĆæĆė2 cm£¬aĆėŹ±£¬µćP”¢µćQĶ¬Ź±øıäĖŁ¶Č£¬µćPµÄĖŁ¶Č±äĪŖĆæĆėb cm£¬µćQµÄĖŁ¶Č±äĪŖĆæĆėd cm.Ķ¼¢ŚŹĒµćP³ö·¢xĆėŗó”÷APDµÄĆ껿S1(cm2)ÓėŹ±¼äx(Ćė)µÄŗÆŹż¹ŲĻµĶ¼Ļó£»Ķ¼¢ŪŹĒµćQ³ö·¢xĆėŗó”÷AQDµÄĆ껿S2(cm2)ÓėŹ±¼äx(Ćė)µÄŗÆŹż¹ŲĻµĶ¼Ļó£®

(1)²ĪÕÕĶ¼¢Ś£¬Ēóa”¢ b¼°Ķ¼¢ŚÖŠcµÄÖµ£»
(2)ĒódµÄÖµ£»
(3)ÉčµćPĄėæŖµćAµÄĀ·³ĢĪŖy1(cm)£¬µćQµ½µćA»¹ŠčŅŖ×ßµÄĀ·³ĢĪŖy2(cm)£¬Ēė·Ö±šŠ“³öøıäĖŁ¶Čŗó£¬y1”¢y2Óė³ö·¢ŗóµÄŌĖ¶ÆŹ±¼äx(Ćė)µÄŗÆŹż¹ŲĻµŹ½£¬²¢Ēó³öµćP”¢µćQĻąÓöŹ±xµÄÖµ£»
(4)µ±µćQ³ö·¢__ __ĆėŹ±£¬µćQµÄŌĖ¶ÆĀ·³ĢĪŖ25 cm.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µćAĪŖŗÆŹży= ![]() £Øx£¾0£©Ķ¼ĻóÉĻŅ»µć£¬Į¬½įOA£¬½»ŗÆŹży=
£Øx£¾0£©Ķ¼ĻóÉĻŅ»µć£¬Į¬½įOA£¬½»ŗÆŹży= ![]() £Øx£¾0£©µÄĶ¼ĻóÓŚµćB£¬µćCŹĒxÖįÉĻŅ»µć£¬ĒŅAO=AC£¬Ōņ”÷ABCµÄĆ껿ĪŖ £®
£Øx£¾0£©µÄĶ¼ĻóÓŚµćB£¬µćCŹĒxÖįÉĻŅ»µć£¬ĒŅAO=AC£¬Ōņ”÷ABCµÄĆ껿ĪŖ £® 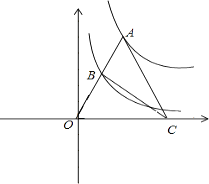
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠµČŹ½³ÉĮ¢µÄŹĒ£Ø £©
A. £Ø-a-b£©2+£Øa-b£©2=-4ab B. £Ø-a-b£©2+£Øa-b£©2=a2+b2
C. £Ø-a-b£©£Øa-b£©=£Øa-b£©2 D. £Ø-a-b£©£Øa-b£©=b2-a2
”¾“š°ø”æD
”¾½āĪö”æ½āĪö£ŗ”ߣØ-a-b£©2+£Øa-b£©2=£Øa+b£©2+£Øa-b£©2=£Øa2+2ab+b2£©+£Øa2-2ab+b2£©=2a2+2b2£¬
”ąŃ”ĻīAÓėŃ”ĻīB“ķĪó£»
”ߣØ-a-b£©£Øa-b£©=-£Øa+b£©£Øa-b£©=-£Øa2-b2£©=b2-a2£¬”ąŃ”ĻīC“ķĪó£¬Ń”ĻīDÕżČ·.
¹ŹŃ”D.
”¾ĢāŠĶ”æµ„Ń”Ģā
”¾½įŹų”æ
8
”¾ĢāÄæ”æČōx=1£¬y=![]() £¬Ōņx2+4xy+4y2µÄÖµŹĒ£Ø £©
£¬Ōņx2+4xy+4y2µÄÖµŹĒ£Ø £©
A. 2 B. 4 C. 32 D. 12
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ę½ŠŠĖıߊĪABCDµÄÖܳ¤ŹĒ26cm£¬¶Ō½ĒĻßACÓėBD½»ÓŚµćO£¬AC”ĶAB£¬EŹĒBCÖŠµć£¬”÷AODµÄÖܳ¤±Č”÷AOBµÄÖܳ¤¶ą3cm£¬ŌņAEµÄ³¤¶ČĪŖ£Ø £© 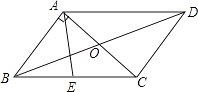
A.3cm
B.4cm
C.5cm
D.8cm
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌĶĮĻĀĮŠ²ÄĮĻ²¢»Ų“šĪŹĢā£ŗ ²ÄĮĻ1£ŗČē¹ūŅ»øöČż½ĒŠĪµÄČż±ß³¤·Ö±šĪŖa£¬b£¬c£¬¼Ē ![]() £¬ÄĒĆ“Čż½ĒŠĪµÄĆ껿ĪŖ
£¬ÄĒĆ“Čż½ĒŠĪµÄĆ껿ĪŖ ![]() £® ¢Ł
£® ¢Ł
¹ÅĻ£Ą°¼øŗĪѧ¼Ņŗ£Ā×£ØHeron£¬Ō¼¹«ŌŖ50Äź£©£¬ŌŚŹżŃ§Ź·ÉĻŅŌ½ā¾ö¼øŗĪ²āĮæĪŹĢā¶ųĪÅĆū£®ĖūŌŚ”¶¶ČĮæ”·Ņ»ŹéÖŠ£¬øų³öĮĖ¹«Ź½¢ŁŗĶĖüµÄÖ¤Ć÷£¬ÕāŅ»¹«Ź½³Ęŗ£Ā×¹«Ź½£®
ĪŅ¹śÄĻĖĪŹżŃ§¼ŅĒŲ¾ÅÉŲ£ØŌ¼1202©©Ō¼1261£©£¬ŌųĢį³öĄūÓĆČż½ĒŠĪµÄČż±ßĒóĆ껿µÄĒŲ¾ÅÉŲ¹«Ź½£ŗ ![]() £® ¢Ś
£® ¢Ś
ĻĀĆęĪŅĆĒ¶Ō¹«Ź½¢Ś½ųŠŠ±äŠĪ£ŗ ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() £®
£®
ÕāĖµĆ÷ŗ£Ā×¹«Ź½ÓėĒŲ¾ÅÉŲ¹«Ź½ŹµÖŹÉĻŹĒĶ¬Ņ»¹«Ź½£¬ĖłŅŌĪŅĆĒŅ²³Ę¢ŁĪŖŗ£Āש©ĒŲ¾ÅÉŲ¹«Ź½£®
ĪŹĢā£ŗČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=13£¬BC=12£¬AC=7£¬”ŃOÄŚĒŠÓŚ”÷ABC£¬ĒŠµć·Ö±šŹĒD”¢E”¢F£®
£Ø1£©Ēó”÷ABCµÄĆ껿£»
£Ø2£©Ēó”ŃOµÄ°ė¾¶£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com