
【题目】如图所示,平面直角坐标的原点是等边三角形的中心,A(0,1),把△ABC绕点O顺时针旋转,每秒旋转60°,则第2017秒时,点A的坐标为( )

A. (0,1) B. (﹣![]() ,﹣
,﹣![]() ) C. (
) C. (![]() ,
,![]() ) D. (
) D. (![]() ,﹣
,﹣![]() )
)
【答案】C
【解析】
△ABC绕点O顺时针旋转一周需6秒,而2017=6×336+1,所以第2017秒时,点A旋转到点A′,如图,则∠AOA′=60°,OA=OA′=1,作A′H⊥x轴于H,然后通过解直角三角形求出A′H和OH即可得到A′点的坐标.
∵360°÷60°=6,
2017=6×336+1,
∴第2017秒时,点A旋转到点A′,如图,
∠AOA′=60°,OA=OA′=1,
作A′H⊥x轴于H,
∵∠A′OH=30°,
∴A′H=![]() OA′=
OA′=![]() ,OH=
,OH=![]() A′H=
A′H=![]() ,
,
∴A′(![]() ,
,![]() ).
).

故答选:C
本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.


科目:初中数学 来源: 题型:
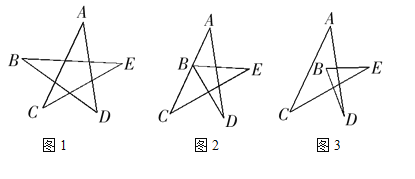
【题目】如图1,有一个五角星ABCDE,你能说明∠A+∠B+∠C+∠D+∠E=![]() 吗? 如图2、图3,如果点B向右移到AC上,或AC的另一侧时,上述结论仍然成立吗?请分别说明理由.
吗? 如图2、图3,如果点B向右移到AC上,或AC的另一侧时,上述结论仍然成立吗?请分别说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
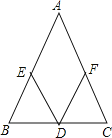
【题目】如图,在△ABC中,D是BC边上的中点,∠BDE=∠CDF,请你添加一个条件,使DE=DF成立.
(1)你添加的条件是
(2)在(1)的条件下,不再添加辅助线和字母,证明DE=DF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这个分式为“和谐分式”
(1)下列分式中, 是和谐分式(填序号即可)
①![]() ②
②![]() ③
③![]() ④
④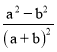
(2)若![]() 为正整数,且
为正整数,且![]() 为和谐分式,请写出所有
为和谐分式,请写出所有![]() 的值
的值
(3)在化简![]() 时,
时,
小强进行了如下三步变形:
原式=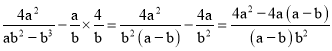
请你接着小强的方法完成化简.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用三角尺可按如图所示的方法画角平分线:已知∠AOB,把一个三角尺的一个顶点放在点O处,一条直角边放在OB上,过直角顶点C作OB的垂线DC;再用同样的方法作OA的垂线EF, EF与DC交于点P.作射线OP,则OP即为∠AOB的平分线.这样作图的依据是构造两个三角形全等,由作法可知,△EPO≌△CPO的依据是( ).
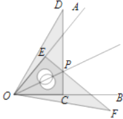
A.SASB.HLC.ASAD.SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了贯彻落实市委政府提出的“精准扶贫”精神,某校特制定了一系列帮扶A、B两贫困村的计划,现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如表:
车型 | 目的地 | |
A村(元/辆) | B村(元/辆) | |
大货车 | ||
800 | 900 | |
小货车 | 400 | 600 |
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区环保局在检查该地区某铝厂时发现,该厂污水严重影响周围环境,要求做定期整改,据估测,该厂年排放污水量为36万吨,接到通知后,该厂决定分两期投入治理,一方面对排放的污水进行处理,同时使得处理后的污水年排放量减少到17.64万吨,如果每期治理中污水减少的百分率相同.
(1)问每期减少的百分率为多少?
(2)如果第一期治理中每减少排放1万吨污水,需投入2万元,第二期每减少排放1万吨污水,需投入3万元,问预计两期治理共需多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四根长度分别为3,4,5,x(x为正整数)的木棒,从中任取三根,首尾顺次相接都能组成一个三角形则组成的三角形的周长( )
A.最小值是11B.最小值是12C.最大值是14D.最大值是15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com