
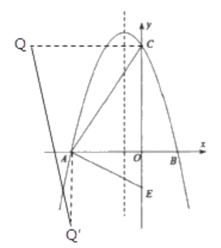
【题目】如图所示,在平面直角坐标系中,二次函数y=ax2+bx+6(a≠0)交x轴于A(﹣4,0),B(2,0),在y轴上有一点E(0,﹣2),连接AE.
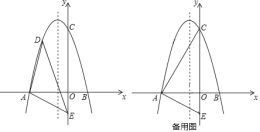
(1)求二次函数的表达式;
(2)点D是第二象限内的抛物线上一动点.
①求△ADE面积最大值并写出此时点D的坐标;
②若tan∠AED=![]() ,求此时点D坐标;
,求此时点D坐标;
(3)连接AC,点P是线段CA上的动点,连接OP,把线段PO绕着点P顺时针旋转90°至PQ,点Q是点O的对应点.当动点P从点C运动到点A,则动点Q所经过的路径长等于 (直接写出答案).
【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+6;(2)①当m=﹣
x+6;(2)①当m=﹣![]() 时,S△ADE的面积最大,最大值为
时,S△ADE的面积最大,最大值为![]() ;点D点坐标为(
;点D点坐标为(![]() ,
,![]() );②D(
);②D(![]() ,
,![]() );(3)2
);(3)2![]() .
.
【解析】
(1)把点A(﹣4,0),B(2,0)代入y=ax2+bx+6的解析式即可得解;
(2)①由A、E两点坐标得出直线AE解析式,设点D坐标为(m,﹣![]() m2﹣
m2﹣![]() m+6,过点D作DK⊥y轴交于点K,然后构建S△ADE面积与m的二次函数,即可得出△ADE面积最大值和点D的坐标;
m+6,过点D作DK⊥y轴交于点K,然后构建S△ADE面积与m的二次函数,即可得出△ADE面积最大值和点D的坐标;
②过点A作AN⊥DE,DE与x轴交于点F,通过证明Rt△AFN∽Rt△EFO,得出![]() ,得到点F的坐标,进而得出直线EF的解析式,联立直线和二次函数,得出点D的坐标即可;
,得到点F的坐标,进而得出直线EF的解析式,联立直线和二次函数,得出点D的坐标即可;
(3)根据题意,当P点在A点时,![]() (﹣4,﹣4),当P点在C点时,Q(﹣6,6),动点Q所经过的路径是线段Q
(﹣4,﹣4),当P点在C点时,Q(﹣6,6),动点Q所经过的路径是线段Q![]() ,求出两点之间的距离即可得解.
,求出两点之间的距离即可得解.
(1)将A(﹣4,0),B(2,0)代入y=ax2+bx+6(a≠0),
![]() ,
,
可得 ,
,
∴y=﹣![]() x2﹣
x2﹣![]() x+6,
x+6,
故答案为:y=﹣![]() x2﹣
x2﹣![]() x+6;
x+6;
(2)①∵A(﹣4,0),E(0,﹣2),
设D(m,﹣![]() m2﹣
m2﹣![]() m+6),
m+6),
过点D作DK⊥y轴交于点K,
K(0,﹣![]() m2﹣
m2﹣![]() m+6),
m+6),
S△ADE=S梯形DKOA+S△AOE﹣S△KED
=![]() ×(KD+AO)×OK+
×(KD+AO)×OK+![]() ×AO×OE﹣
×AO×OE﹣![]() ×KD×KE
×KD×KE
=![]() (﹣m+4)×(﹣
(﹣m+4)×(﹣![]() m2﹣
m2﹣![]() m+6)+
m+6)+![]() ×4×2﹣
×4×2﹣![]() ×(﹣m)×(2﹣
×(﹣m)×(2﹣![]() m2﹣
m2﹣![]() m+6)
m+6)
=﹣![]() (m+
(m+![]() )2+
)2+![]() ,
,
当m=﹣![]() 时,S△ADE的面积最大,最大值为
时,S△ADE的面积最大,最大值为![]() ,点D点坐标为(
,点D点坐标为(![]() ,
,![]() ),
),
故答案为: ![]() ;(
;(![]() ,
,![]() );
);
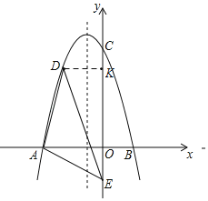
②过点A作AN⊥DE,DE与x轴交于点F,
∵tan∠AED=![]() ,
,
∴AN=![]() ,NE=3
,NE=3![]() ,
,
Rt△AFN∽Rt△EFO,
∴![]() ,
,
∵EF2=OF2+4,
∴NF=3![]() ﹣EF,
﹣EF,
∴![]() =
=![]() ,
,
∴OF=2,
∴F(﹣2,0),
∴EF直线解析式为y=﹣x﹣2,
∴﹣x﹣2=﹣![]() x2﹣
x2﹣![]() x+6时,x=
x+6时,x=![]() ,
,
∴D(![]() ,
,![]() ),
),
故答案为:D(![]() ,
,![]() );
);
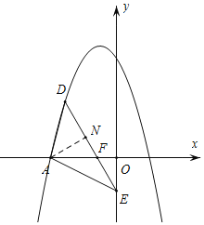
(3)∵Q点随P点运动而运动,P点在线段AC上运动,
∴Q点的运动轨迹是线段,
当P点在A点时,![]() (﹣4,﹣4),
(﹣4,﹣4),
当P点在C点时,Q(﹣6,6),
∴Q点的轨迹长为Q![]() =
=![]() =2
=2![]() ,
,
故答案为:2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
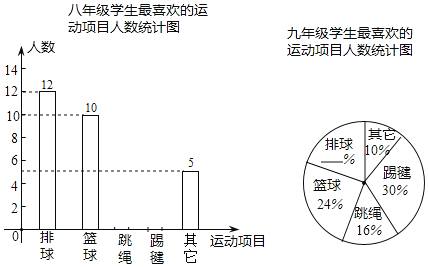
【题目】通辽市某中学为了了解学生“大课间”活动情况,在七、八、九年级的学生中,分别抽取了相同数量的学生对“你最喜欢的运动项目”进行调查(每人只能选一项),调查结果的部分数据如下表(图)所示,其中七年级最喜欢跳绳的人数比八年级多5人,九年级最喜欢排球的人数为10人.
七年级学生最喜欢的运动项目人数统计表
项目 | 排球 | 篮球 | 踢毽 | 跳绳 | 其他 |
人数(人) | 7 | 8 | 14 |
| 6 |
请根据以上统计表(图)解答下列问题:
(1)本次调查共抽取了多少人?
(2)补全统计表和统计图.
(3)该校有学生1800人,学校想对“最喜欢踢毽子”的学生每4人提供一个毽子,学校现有124个毽子,能否够用?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场准备采购一批特色商品,经调查,用5000元采购![]() 型商品的件数是用2000元采购
型商品的件数是用2000元采购![]() 型商品的件数的2倍,一件
型商品的件数的2倍,一件![]() 型商品的进价比一件
型商品的进价比一件![]() 型商品的进价多10元.
型商品的进价多10元.
(1)求一件![]() ,
,![]() 型商品的进价分别为多少元?
型商品的进价分别为多少元?
(2)若该商场购进![]() ,
,![]() 型商品共200件进行试销,其中
型商品共200件进行试销,其中![]() 型商品的件数不大于
型商品的件数不大于![]() 型商品的件数,且不小于80件.已知
型商品的件数,且不小于80件.已知![]() 型商品的售价为80元/件,
型商品的售价为80元/件,![]() 型商品的售价为60元/件,且
型商品的售价为60元/件,且![]() ,
,![]() 型商品均全部售出.设购进
型商品均全部售出.设购进![]() 型商品
型商品![]() 件,求该商场销售完这批商品的利润
件,求该商场销售完这批商品的利润![]() 与
与![]() 之间的函数关系式,并写出
之间的函数关系式,并写出![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,商场决定在试销活动中每售出一件![]() 型商品,就从一件
型商品,就从一件![]() 型商品的利润中捐献慈善资金
型商品的利润中捐献慈善资金![]() 元
元![]() ,若该商场售完
,若该商场售完![]() 、
、![]() 型所有商品并捐献资金后获得的最大收益是4800元,求出
型所有商品并捐献资金后获得的最大收益是4800元,求出![]() 值.
值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=![]() x-2与反比例函数y=
x-2与反比例函数y=![]() 的图象相交于点A(2, n) ,与x轴相交于点B.
的图象相交于点A(2, n) ,与x轴相交于点B.
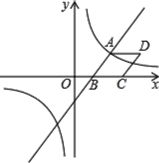
(1)求k 的值以及点 B 的坐标;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)在y轴上是否存在点P,使PA+PB的值最小?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人加工同一种零件,甲每天加工的数量是乙每天加工数量的1.5倍,两人各加工300个这种零件,甲比乙少用5天.
(1)求甲、乙两人每天各加工多少个这种零件?
(2)已知甲、乙两人加工这种零件每天的加工费分别是150元和120元,现有1500个这种零件的加工任务,甲单独加工一段时间后另有安排,剩余任务由乙单独完成.如果总加工费为7800元,那么甲、乙各加工了多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 与一次函数
与一次函数![]() 的图象相交于点A、点D,且点A的横坐标为1,点D的纵坐标为-1,过点A作AB⊥x轴于点B,△AOB的面积为1.
的图象相交于点A、点D,且点A的横坐标为1,点D的纵坐标为-1,过点A作AB⊥x轴于点B,△AOB的面积为1.
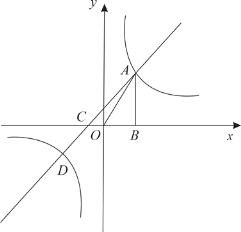
(1)求反比例函数和一次函数的解析式;
(2)若一次函数y=ax+b的图像与x轴交于点C,求∠ACO的度数.
(3)结合图像直接写出,当![]() 时,x的取值范围.
时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有![]() 四张不透明的卡片,除正面上的图案不同外,其他均相同,将这四张卡片背 面向上洗匀后放在桌面上.
四张不透明的卡片,除正面上的图案不同外,其他均相同,将这四张卡片背 面向上洗匀后放在桌面上.
(1)从中随机取出一张卡片,卡片上的图案是中心对称图形的概率是_____;
(2)若从四张卡片中随机拿出两张卡片,请用画树状图或列表的方法,求抽取的两张卡片都是轴对称图形的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了创建书香校园,去年购买了一批图书.其中科普书的单价比文学书的单价多8元,用1800元购买的科普书的数量与用l000元购买的文学书的数量相同.
(1)求去年购买的文学书和科普书的单价各是多少元;
(2)这所学校今年计划再购买这两种文学书和科普书共200本,且购买文学书和科普书的总费用不超过2088元.今年文学书的单价比去年提高了20%,科普书的单价与去年相同,且每购买1本科普书就免费赠送1本文学书,求这所学校今年至少要购买多少本科普书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与
与![]() 轴和
轴和![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() 抛物线
抛物线![]() 经过点
经过点![]() 与直线
与直线![]() 的另一个交点为
的另一个交点为![]() .
.
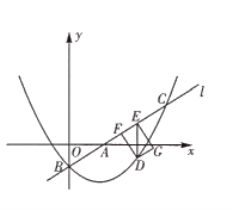
![]() 求
求![]() 的值和抛物线的解析式
的值和抛物线的解析式
![]() 点
点![]() 在抛物线上,
在抛物线上,![]() 轴交直线
轴交直线![]() 于点
于点![]() 点
点![]() 在直线
在直线![]() 上,且四边形
上,且四边形![]() 为矩形.设点
为矩形.设点![]() 的横坐标为
的横坐标为![]() 矩形
矩形![]() 的周长为
的周长为![]() 求
求![]() 与
与![]() 的函数关系式以及
的函数关系式以及![]() 的最大值
的最大值
![]() 将
将![]() 绕平面内某点
绕平面内某点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() (点
(点![]() 分别与
分别与![]() 点对应),若
点对应),若![]() 的两个顶点恰好落在抛物线上,请直接写出点
的两个顶点恰好落在抛物线上,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com