
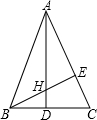
 如图,在△ABC中,AB=AC,AD和BE是高,它们交于点H,且AE=BE.求证:
如图,在△ABC中,AB=AC,AD和BE是高,它们交于点H,且AE=BE.求证:分析 (1)根据高的定义求出∠ADC=∠BEC=90°,根据三角形的内角和定理求出∠CAD=∠CBE,根据等腰三角形的性质求出∠BAC=2∠CAD=2∠BAD即可;
(2)根据ASA推出△AEH≌△BEC,根据全等三角形的性质得出AH=BC,根据等腰三角形的性质得出BC=2BD即可.
解答 证明:(1)∵AD和BE是高,
∴∠ADC=∠BEC=90°,
∴∠C+∠CAD=90°,∠C+∠CBE=90°,
∴∠CAD=∠CBE,
∵AB=AC,AE是高,
∴∠BAC=2∠CAD=2∠BAD,
∴∠BAC=2∠CBE;
(2)∵AD和BE是高,
∴∠AEH=∠BEC=90°,
在△AEH和△BEC中,
$\left\{\begin{array}{l}{∠EAH=∠CBE}\\{AE=BE}\\{∠AEH=∠BEC}\end{array}\right.$,
∴△AEH≌△BEC(ASA),
∴AH=BC,
∵AB=AC,AD是高,
∴BC=2BD,
∴AH=2BD.
点评 本题考查了三角形内角和定理,等腰三角形的性质和判定,全等三角形的性质和判定的应用能综合运用性质进行推理是解此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 8 | C. | 9 | D. | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
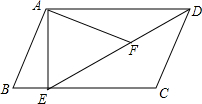 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y=-x2+bx+c交x轴于C(1,0),D(3,0)两点(点C在点D的左侧),点A为抛物线的顶点.
已知抛物线y=-x2+bx+c交x轴于C(1,0),D(3,0)两点(点C在点D的左侧),点A为抛物线的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com