
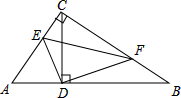
 在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,E,F分别是AC,BC边上一点.
在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,E,F分别是AC,BC边上一点.分析 (1)证相关线段所在的三角形相似即可,即证Rt△ADC∽Rt△CDB;
(2)易证得CE:BF=AC:BC,联立(1)的结论,即可得出CE:BF=CD:BD,由此易证得△CED∽△BFD,即可得出∠CDE=∠BDF,由于∠BDF和∠CDF互余,则∠EDC和∠CDF也互余,由此可求得∠EDF的度数.
解答 解:(1)∵CD⊥AB,
∴∠A+∠ACD=90°
又∵∠A+∠B=90°
∴∠B=∠ACD
∴Rt△ADC∽Rt△CDB
∴$\frac{AC}{BC}$=$\frac{CD}{BD}$;
(2)∵$\frac{CE}{BF}$=$\frac{\frac{1}{3}AC}{\frac{1}{3}BC}$=$\frac{AC}{BC}$,
又∵∠ACD=∠B,
∴△CED∽△BFD;
∴∠CDE=∠BDF;
∴∠EDF=∠EDC+∠CDF=∠BDF+∠CDF=∠CDB=90°.
点评 此题考查的是相似三角形的判定和性质;识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角,可利用数形结合思想根据图形提供的数据计算对应角的度数、对应边的比.


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,根据道路管理规定,直线l的路段上行驶的车辆,限速60千米/时,已知测速站点M距离直线l的距离MN为30米(如图所示),现有一辆汽车匀速行驶,测得此车从A点行驶到B点所用时间为6秒,∠AMN=60°,∠BMN=45°.
如图,根据道路管理规定,直线l的路段上行驶的车辆,限速60千米/时,已知测速站点M距离直线l的距离MN为30米(如图所示),现有一辆汽车匀速行驶,测得此车从A点行驶到B点所用时间为6秒,∠AMN=60°,∠BMN=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com